1. ライブラリ
from scipy.stats import norm
import numpy as np
import matplotlib.pyplot as plt
2. 折れ線グラフのデータと描画
x = np.array([
0, 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, 11,
12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23,
24, 25, 26, 27
])
y = np.array([
834.62503163, 817.98478513, 710.48150374, 551.69349748,
396.92652116, 262.13219174, 181.69726178, 128.23167309,
90.96796944, 67.15919026, 53.77332502, 41.19329868,
40.05760777, 50.90585954, 58.73682089, 61.47107074,
59.73455969, 51.22381365, 42.67081755, 38.29234283,
39.32761033, 46.44809404, 53.99442401, 55.60249625,
48.20150074, 38.97137638, 35.40707449, 44.28240572
])
plt.plot(x[1:], y[1:], label=f'Signal')3. 最尤推定で正規分布によるFittingと描画
# Fittingはヒストグラムを描画できるデータ形式に対して実施するため、模擬データを作成
data = []
for i, v in enumerate(y[:10]): # 右裾が重いためx=10までをFittingに使用
data.extend([i + 0.5] * round(v)) # x=iについてy(x)個のデータを生成することでヒストグラムのデータを生成
data.extend([-1 * (i + 0.5)] * round(v)) # x<0領域にもデータを用意する
param = norm.fit(data) # Fitting
pdf_fitted = norm.pdf(x,loc=param[0], scale=param[1]) # 推定したパラメタで密度関数を作成
coef = y[0] / pdf_fitted[0] # 密度関数は全面積が1となる。高さを元の曲線に合わせるための係数を算出
plt.plot(x, pdf_fitted * coef, label=f'Fitted') # 密度関数 * 係数で描画
plt.scatter([param[1]], [norm.pdf(param[1],loc=param[0], scale=param[1]) * coef], s=300, marker='*') # ついでに変曲点も★でプロット4. プロット
# プロット設定
plt.ylim(0, y_max) # y軸スケール固定
plt.axhline(0, 0, 1, c='black') # y軸の描画
plt.axvline(0, 0, 1, c='black') # x軸の描画
plt.legend() # レジェンドの追加
plt.title(f'Signal intensity') # タイトル
# 先に保存してから描画
plt.savefig(f'signal_intensity.png')
plt.show()
5. 描画結果
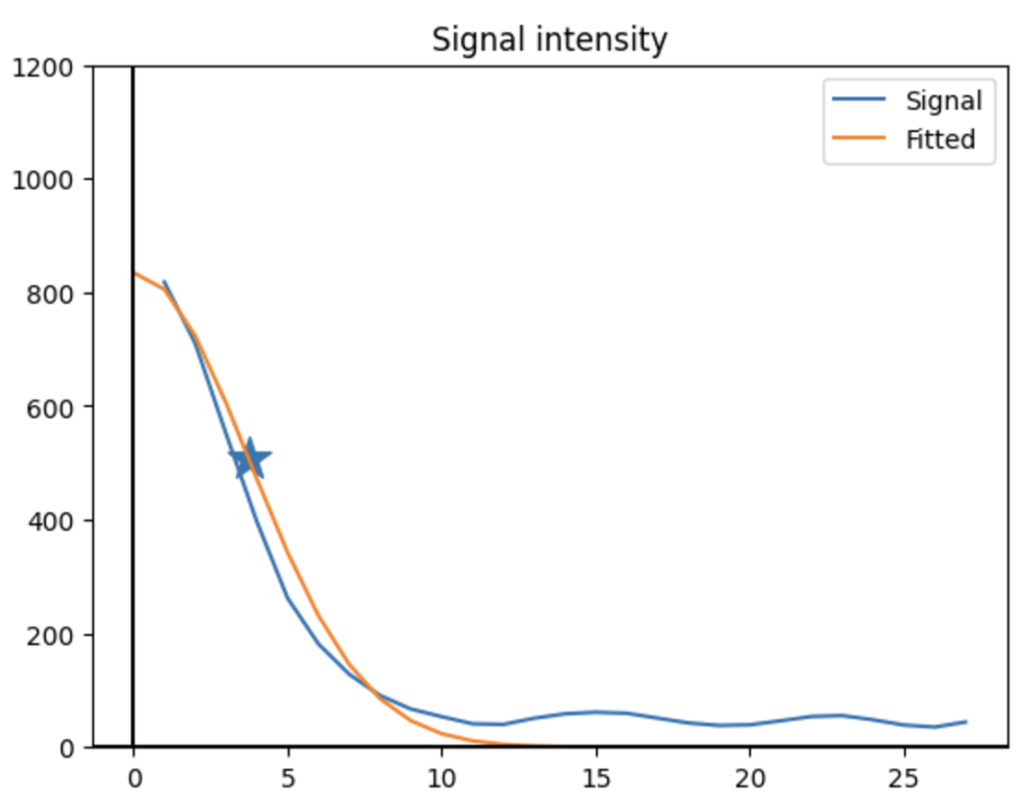




コメント