1. 正射影ベクトル
(1) 様々なベクトル(7):正射影ベクトルの定義
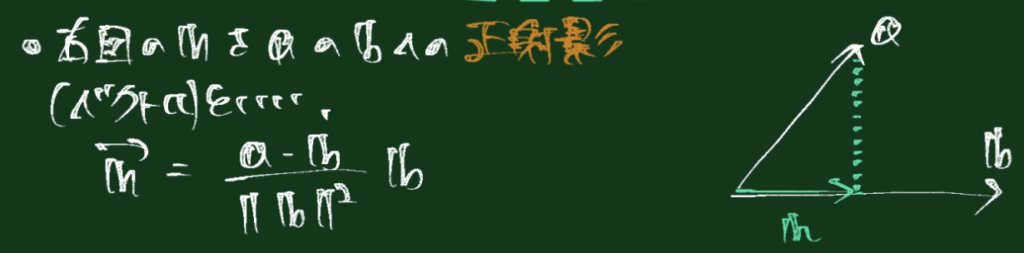
(2) 正射影ベクトルの公式
正射影ベクトルは$\mathbf{a}$と$\mathbf{b}$を用いて以下のように表現できます。
ベクトル $\mathbf{a}$ をベクトル $\mathbf{b}$ の張る直線($\operatorname{span}{\mathbf{b}}$(=$\mathbf{b}$を方向ベクトルとした直線))に正射影したベクトル(直交射影)は
$$\mathrm{proj}_{\mathbf{b}}\mathbf{a}=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{b}|^2}\,\mathbf{b}$$
で与えられます。対応するスカラー射影(符号つき長さ)は
$$\mathrm{sproj}_{\mathbf{b}}\mathbf{a}=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{b}|}.$$
で与えられます。
※ $\operatorname{span}$については以下の記事を参照して下さい。
証明をみる (幾何学的な証明)
$\mathbf{a}$ と $\mathbf{b}$ のなす角を $\theta$ とすると、$\mathbf{a}$ の $\mathbf{b}$ 方向の「長さ(スカラー)」は $$ \|\mathbf{a}\|\cos\theta $$ 正射影ベクトル$\mathrm{proj}_{\mathbf{b}}\mathbf{a}$は$\mathbf{b}$の単位ベクトルを上記のスカラー倍すれば得られるから、 $$ \mathrm{proj}_{\mathbf{b}}\mathbf{a}=\frac{\|\mathbf{a}\|\cos\theta}{\|\mathbf{b}\|}\,\mathbf{b} $$ 内積の公式 $\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta$ を用いれば $$ \begin{align} \frac{\|\mathbf{a}\|\cos\theta}{\|\mathbf{b}\|}\,\mathbf{b} &=\frac{\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta}{\|\mathbf{b}\|^2}\,\mathbf{b} \\ &=\frac{\mathbf{a}\cdot\mathbf{b}}{\|\mathbf{b}\|^2}\,\mathbf{b} \end{align} $$ と一致します。証明をみる (直交分解を用いた証明)
$\mathbf{b}\neq\mathbf{0}$ とします。$\mathbf{a}$ を $\mathbf{b}$ に平行な成分と $\mathbf{b}$ に直交する成分に分解できると仮定します: $$\mathbf{a}=\lambda\mathbf{b}+\mathbf{w},\qquad \mathbf{w}\perp\mathbf{b}.$$ 両辺を $\mathbf{b}$ と内積を取ると $$ \mathbf{a}\cdot\mathbf{b}=\lambda\,|\mathbf{b}|^2+\underbrace{\mathbf{w}\cdot\mathbf{b}}_{=0} =\lambda\,|\mathbf{b}|^2. $$ よって $$ \lambda=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{b}|^2},\qquad \lambda\mathbf{b}=\frac{\mathbf{a}\cdot\mathbf{b}}{|\mathbf{b}|^2}\,\mathbf{b}. $$ これが $\mathbf{a}$ の $\operatorname{span}{\mathbf{b}}$ への直交射影。直交分解は一意なので上式が成り立ちます。$\square$直交分解については以下の記事を参照。
2. 直線のベクトル方程式
(1) ベクトルによる直線の方程式
証明をみる
$L$ 上の任意の点 $\mathbf{r}$ は基準点 $\mathbf{p}_0$ から方向 $\mathbf{d}$ に実数倍だけ進んだ位置に限られるので $\mathbf{r}-\mathbf{p}_0=t\mathbf{d}$ すなわち上式。逆に上式の形の点はすべて $L$ に属します。$\square$(2) 空間の直線の方程式
証明をみる
成分比較より $x=x_0+at,\ y=y_0+bt,\ z=z_0+ct$。$a,b,c\neq0$ ならば各式を $t$ について解き,3つが一致することが点の条件。$a=0$ なら $x=x_0$ が付加され,残り2つで $t$ を消去します。$\square$(3) まとめ

3. 平面のベクトル方程式
(1) ベクトルによる平面の方程式
証明をみる
$\Pi$ 内の任意の点は $\mathbf{p}_0$ から $\mathbf{u}$ と $\mathbf{v}$ の線形結合で一意に到達できることから明らかです。$\square$(2) 平面の方程式
証明をみる
$\mathbf{r}-\mathbf{p}_0$ は $\Pi$ 内のベクトルなので $\mathbf{n}$ と直交し,内積が $0$。成分表示すれば右式が得られます。$\square$(3) まとめ

4. 三角形の面積
以降,三角形の 3 辺長を $a,b,c$,対応する角を $A,B,C$,半周長を $s=(a+b+c)/2$,外接円半径を $R$,内接円半径を $r$ とします。ベクトル表示では 2 辺を $\mathbf{u},\mathbf{v}$ とします。
(1) 底辺と高さから求める公式
底辺を $b$,その高さを $h$ とすると $$S=\frac{1}{2}bh.$$
証明をみる
底辺 $b$ を一辺とする平行四辺形の面積は $bh$。三角形はその半分。$\square$(2) $\sin$ を用いた公式
2 辺 $a,b$ とその間の角を $\theta$ とすると $$S=\frac{1}{2}ab\sin\theta.$$
証明をみる
底辺を $a$ とすると高さは $b\sin\theta$ なので $S=\tfrac12 a(b\sin\theta)$。$\square$(3) 内接円の半径を用いた公式
$$S=rs.$$
証明をみる
内心と各点を結ぶ線分によって三角形は 3 つの三角形に分割される。各小三角形の高さはいずれも $r$ で,底辺はそれぞれ $a,b,c$ なので総和は $$S=\tfrac12 ar+\tfrac12 br+\tfrac12 cr=\tfrac12(a+b+c)r=rs.\square$$(4) 外接円の半径を用いた公式
$$S=\frac{abc}{4R}.$$
証明をみる
正弦定理 $a=2R\sin A$ 等より $$S=\tfrac12 bc\sin A=\tfrac12\,(2R\sin B)(2R\sin C)\sin A=\frac{(2R)^2}{2}\,\sin A\sin B\sin C.$$ また $a=2R\sin A$ から $\sin A=\tfrac{a}{2R}$ 等を代入すれば $$S=\frac{abc}{4R}.$$ $\square$(5) 座標を用いた公式
3 点 $(x_1,y_1)$,$(x_2,y_2)$,$(x_3,y_3)$ に対し $$ S=\frac12\left| \begin{vmatrix} x_1 & y_1 & 1\\ x_2 & y_2 & 1\\ x_3 & y_3 & 1 \end{vmatrix}\right| =\frac12\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right|. $$
証明をみる
与えられた3点を $$ P_1=(x_1,y_1),\quad P_2=(x_2,y_2),\quad P_3=(x_3,y_3) $$ とする。(1) 成分による公式の証明
平行移動で $P_3$ を原点にしても面積は不変なので、各点を $$ (x_i’,y_i’)=(x_i-x_3,\ y_i-y_3)\quad(i=1,2,3) $$ と置き換えても三角形の面積 $S$ は変わらない。特に $P_3’=(0,0)$ となる。 このとき三角形 $P_1’P_2’P_3’$ の面積は $$ S=\frac12\left|\det\begin{pmatrix} x_1’&y_1’\\ x_2’&y_2′ \end{pmatrix}\right| =\frac12\left|x_1’y_2′-x_2’y_1’\right|. $$ これは、原点 $O$、ベクトル $u=(x_1′,y_1′)^{\mathsf T}$、$v=(x_2′,y_2′)^{\mathsf T}$ が張る平行四辺形の有向面積が $\det[u\ v]$ で与えられ、三角形はその半分であることから従う(幾何または外積の性質)。 $’$ を元の座標に戻すと $$ x_1’=x_1-x_3,\quad y_1’=y_1-y_3,\quad x_2’=x_2-x_3,\quad y_2’=y_2-y_3. $$ ゆえに $$ S=\frac12\left|(x_1-x_3)(y_2-y_3)-(x_2-x_3)(y_1-y_3)\right|. $$ (2) 行列式による公式の証明
$3\times3$ 行列式を考える: $$ \Delta= \begin{vmatrix} x_1&y_1&1\\ x_2&y_2&1\\ x_3&y_3&1 \end{vmatrix}. $$ 第3列で余因子展開すると $$ \Delta= 1\cdot\begin{vmatrix}x_1&y_1\\x_2&y_2\end{vmatrix} -1\cdot\begin{vmatrix}x_1&y_1\\x_3&y_3\end{vmatrix} +1\cdot\begin{vmatrix}x_2&y_2\\x_3&y_3\end{vmatrix}. $$ すなわち $$ \Delta=x_1y_2-x_2y_1-(x_1y_3-x_3y_1)+(x_2y_3-x_3y_2) =x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2). $$ 一方で、行列式の性質(列基本変形)を用いて第1列と第2列からそれぞれ第3列を引いても値は変わらないので $$ \Delta= \begin{vmatrix} x_1-x_3&y_1-y_3&1\\ x_2-x_3&y_2-y_3&1\\ 0&0&1 \end{vmatrix} = \begin{vmatrix} x_1-x_3&y_1-y_3\\ x_2-x_3&y_2-y_3 \end{vmatrix}. $$ よって $$ \Delta=(x_1-x_3)(y_2-y_3)-(x_2-x_3)(y_1-y_3). $$ これを (1) の式と比べると $$ S=\frac12|\Delta| =\frac12\left| \begin{vmatrix} x_1&y_1&1\\ x_2&y_2&1\\ x_3&y_3&1 \end{vmatrix} \right| =\frac12\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right|. $$ (1)(2)により、三角形 $P_1P_2P_3$ の面積 $S$ は $$ S=\frac12\left| \begin{vmatrix} x_1&y_1&1\\ x_2&y_2&1\\ x_3&y_3&1 \end{vmatrix}\right| =\frac12\left|x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\right| $$ であることが示された。□
行列式および余因子展開については以下の記事を参照。
(6) ベクトルの内積を用いた三角形の面積の公式
$$S=\frac12\sqrt{\ |\mathbf{u}|^2\ |\mathbf{v}|^2-\left(\mathbf{u}\cdot\mathbf{v}\right)^2\ }$$
証明をみる
2 辺ベクトルを $\mathbf{u},\mathbf{v}$ とする(三角形の一頂点を共有し,向きを揃える)。 $$S=\frac12|\mathbf{u}|\ |\mathbf{v}|\ \sin\theta,$$ ここで $\theta$ は $\mathbf{u}$ と $\mathbf{v}$ のなす角。内積を用いると $$ \cos\theta=\frac{\mathbf{u}\cdot\mathbf{v}}{|\mathbf{u}|\ |\mathbf{v}|}, \qquad \sin^2\theta=1-\cos^2\theta. $$ よって $$ 4S^2=|\mathbf{u}|^2\ |\mathbf{v}|^2\ \sin^2\theta =|\mathbf{u}|^2\ |\mathbf{v}|^2-\left(\mathbf{u}\cdot\mathbf{v}\right)^2. $$ 両辺の平方根をとり2で割ることで公式が得られる。(7) 外積を用いた公式
三次元で辺ベクトルを $\mathbf{u},\mathbf{v}\in\mathbb{R}^3$ とすると $$S=\frac12|\mathbf{u}\times\mathbf{v}|.$$
証明をみる
$|\mathbf{u}\times\mathbf{v}|=|\mathbf{u}|\,|\mathbf{v}|\sin\theta$ は平行四辺形の面積であり,三角形はその半分。$\square$(8) ヘロンの公式
$$S=\sqrt{s(s-a)(s-b)(s-c)}.$$
証明をみる
$\theta$ を $C$ として $$S^2=\left(\tfrac12 ab\sin C\right)^2=\tfrac14 a^2b^2(1-\cos^2 C).$$ 余弦定理 $c^2=a^2+b^2-2ab\cos C$ より $\cos C=\dfrac{a^2+b^2-c^2}{2ab}$。代入して $$ 16S^2=4a^2b^2-\left(a^2+b^2-c^2\right)^2 =2a^2b^2+2b^2c^2+2c^2a^2-a^4-b^4-c^4. $$ 一方で $(a+b+c)(-a+b+c)(a-b+c)(a+b-c)$ を展開すると同じ式になるため $$16S^2=(a+b+c)(-a+b+c)(a-b+c)(a+b-c)=16\,s(s-a)(s-b)(s-c).$$ 両辺を $16$ で割って平方根を取れば主張が従う。$\square$(9) まとめ

5. 様々なベクトル
(1) 様々なベクトル(8):方向余弦の定義と性質
$\mathbf{v}=(x,y,z)\neq\mathbf{0}$ について$(\cos\alpha,\cos\beta,\cos\gamma)$を方向余弦という。 ただし、 $$ \cos\alpha=\frac{x}{|\mathbf{v}|},\quad \cos\beta=\frac{y}{|\mathbf{v}|},\quad \cos\gamma=\frac{z}{|\mathbf{v}|},\qquad |\mathbf{v}|=\sqrt{x^2+y^2+z^2}. $$ 方向余弦については、以下の性質が成り立つ。 $\cos^2\alpha+\cos^2\beta+\cos^2\gamma=1$。
証明をみる
上式を代入して $\dfrac{x^2+y^2+z^2}{|\mathbf{v}|^2}=1$。$\square$まとめ

(2) 様々なベクトル(9):共面ベクトルの定義と性質
証明をみる
$\mathbf{b}\times\mathbf{c}$ は $\mathbf{b},\mathbf{c}$ を含む平面に垂直。$\mathbf{a}$ が同一平面内なら直交するので内積が $0$。逆に $0$ なら $\mathbf{a}$ はその法線に直交し,同平面に属する。$\square$(3) 様々なベクトル(10):面積ベクトルの定義
まとめ








コメント