ベクトルの導入と演算 - バイオインフォの森

1. ベクトルの定義
2. ベクトルの和と差
3. ベクトルのスカラー倍
4. ベクトルの内積とノルム
5. 外積
7. 1次独立と1次従属
- (1) 1次独立
- (2) 1次従属

1. ベクトルの定義

(1) ベクトルの定義と表記

定義1.1: ベクトル

$a_1, a_2, \cdots, a_n$を$1, 2, 3+i$などの数とすると、ベクトルとは以下のように数を縦に複数を並べたもので、記号としては$\mathbf{a}$のようにボールド体を用いて表します。 $$ \mathbf{a} = \begin{pmatrix} a_1 \\ a_2 \\ \vdots \\ a_n \end{pmatrix} $$ なお、以下のように数を横に並べてベクトルとする場合もありますが、特に縦横の指定がなくベクトルが定義された場合は縦に数字を並べたベクトルと解釈することに注意して下さい。 $$ \mathbf{a’} = (a_1, a_2, \cdots, a_n) $$

$\mathbf{a}$と$\mathbf{a’}$は数学的に異なり、両者を区別するために$\mathbf{a}$を縦ベクトル、$\mathbf{a’}$を横ベクトルと呼びます。後述する行列の考え方を用いると、$\mathbf{a}$は$n$行$1$列の行列で、$\mathbf{a’}$は$1$行$n$列の行列としてはっきり区別されます。

※ より正確に述べますと、単純に数を並べただけではベクトルとは呼びません。後述する和(差)とスカラー倍が決められている場合にベクトルと呼びます。

(2) ベクトルの次元と成分

定義1.2: 次元と成分

並べられた数が$n$個のベクトルは$n$次元のベクトルと呼びます。また、並べられたそれぞれの数はベクトルの成分と言います。

ベクトルの次元と成分を簡潔に表記する方法があります。まず、実数全体の集合を$\mathbb{R}$、複素数全体の集合を$\mathbb{C}$と表記します。また、成分が全て実数の$n$次元ベクトル全体の集合を$\mathbb{R}^n$、成分に複素数を含む$n$次元ベクトル全体の集合を$\mathbb{C}^n$と表記します。このとき、ベクトル$\mathbf{a}$が実数成分の$n$次元ベクトルであること、すなわち$n$次元の実ベクトルであることを$\mathbf{a} \in \mathbb{R}^n$、成分に複素数を含む$n$次元のベクトル、すなわち$n$次元の複素ベクトルであることを$\mathbf{a} \in \mathbb{C}^n$と表記します。

(3) 様々なベクトル(1)：ゼロベクトル

定義1.3: ゼロベクトル

すべての成分が0であるベクトルをゼロベクトルと呼び、$\mathbf{0}$ や $\begin{pmatrix} 0 \\ \vdots \\ 0 \end{pmatrix}$ と表記します。

(4) 様々なベクトル(2)：単位ベクトル

定義1.4: 単位ベクトル

単位ベクトルとは、大きさ（ノルム）が1のベクトルです。
※ ノルムの詳細については定義1.13を参照して下さい。

(5) 様々なベクトル(3)：幾何ベクトル

定義1.5: 幾何ベクトル

2次元または3次元のベクトルは原点からその成分が表す座標への矢印とみなすことが可能であり、その意味でベクトルは大きさと向きを持つ量とも言えます。

このようにベクトルの幾何学的側面を強調して記述する場合、そのベクトルを幾何ベクトルと呼び、$\vec{OA}$のように表します。

(6) 様々なベクトル(4)：位置ベクトル

定義1.6: 位置ベクトル

原点を始点として平面や空間上の点 $P(x, y, z)$ などへのベクトルを特に位置ベクトルと呼び、以下のように表現されます。 $$\mathbf{r} = \begin{pmatrix} x \\ y \\ z \end{pmatrix}$$

(7) 様々なベクトル(5)：方向ベクトル

定義1.7: 方向ベクトル

直線や線分と平行なベクトルを方向ベクトルといいます。

2点 $A(x_1, y_1, z_1)$, $B(x_2, y_2, z_2)$ を通る直線の方向ベクトルは以下です。
$$\vec{AB} = \begin{pmatrix} x_2 – x_1 \\ y_2 – y_1 \\ z_2 – z_1 \end{pmatrix}$$ また、以下の直線の方程式においては方向ベクトルが$\begin{pmatrix} a \\ b \\ c \end{pmatrix}$で与えられます。 $$\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}$$ ※ 空間の直線の方程式の詳細については定理2.4を参照して下さい。

(8) 様々なベクトル(6)：法線ベクトル

定義1.8: 法線ベクトル

ある直線や平面に対して垂直なベクトルを法線ベクトルといいます。

例えば、直線 $ax + by + c = 0$ に対する法線ベクトルは
$$\mathbf{n} = \begin{pmatrix} a \\ b \end{pmatrix}$$ です。
また、平面 $ax + by + cz + d = 0$ に対する法線ベクトルは
$$\mathbf{n} = \begin{pmatrix} a \\ b \\ c \end{pmatrix}$$ です。
※ 平面の方程式の詳細については定理2.5を参照して下さい。

2. ベクトルの和と差

(1) ベクトル和の定義

定義1.9: ベクトルの和

$\mathbf{a} \in \mathbb{C}^n$と$\mathbf{b} \in \mathbb{C}^m$の和は次元が等しい場合、つまり$n=m$場合に定義され$\mathbf{a}+\mathbf{b}$と表記し、その成分は対応する成分の和とします。

すなわち、$\mathbf{a}=\begin{pmatrix}a_1\\ \vdots \\ a_n\end{pmatrix}$, $\mathbf{b}=\begin{pmatrix}b_1 \\ \vdots \\ b_n \end{pmatrix}$とすると、$\mathbf{a}$と$\mathbf{b}$の和は以下です。

$$ \mathbf{a} + \mathbf{b} = \begin{pmatrix} a_1 + b_1 \\ \vdots \\ a_n + b_n \end{pmatrix} $$

(2) ベクトルの差の定義

定義1.10: ベクトルの差

$\mathbf{a} \in \mathbb{C}^n$と$\mathbf{b} \in \mathbb{C}^m$の差は次元が等しい場合、つまり$n=m$場合に定義され$\mathbf{a}-\mathbf{b}$と表記し、その成分は対応する成分の差とします。

$$ \mathbf{a} – \mathbf{b} = \begin{pmatrix} a_1 – b_1 \\ \vdots \\ a_n – b_n \end{pmatrix} $$

(3) 和(差)の性質

交換法則

$\mathbf{a}, \mathbf{b} \in \mathbb{C}^n$について、以下が成立します。

$$\mathbf{a} + \mathbf{b} = \mathbf{b} + \mathbf{a}$$

証明をみる

$\mathbf{a}=\begin{pmatrix}a_1\\ \vdots \\ a_n\end{pmatrix}$, $\mathbf{b}=\begin{pmatrix}b_1 \\ \vdots \\ b_n \end{pmatrix}$とすると、 $$ \begin{align} \mathbf{a} + \mathbf{b} &= \begin{pmatrix}a_1+b_1\\ \vdots \\ a_n+b_n\end{pmatrix} \\ &= \begin{pmatrix}b_1+a_1\\ \vdots \\ b_n+a_n\end{pmatrix} \\ &= \mathbf{b} + \mathbf{a} \end{align} $$ より、成立します。

結合法則

$\mathbf{a}, \mathbf{b}, \mathbf{c} \in \mathbb{C}^n$について、以下が成立します。 $$(\mathbf{a} + \mathbf{b}) + \mathbf{c} = \mathbf{a} + (\mathbf{b} + \mathbf{c})$$

証明をみる

$\mathbf{a}=\begin{pmatrix}a_1\\ \vdots \\ a_n\end{pmatrix}$, $\mathbf{b}=\begin{pmatrix}b_1 \\ \vdots \\ b_n \end{pmatrix}$, $\mathbf{c}=\begin{pmatrix}c_1 \\ \vdots \\ c_n \end{pmatrix}$とすると $$ \begin{align} (\mathbf{a} + \mathbf{b}) + \mathbf{c} &= \begin{pmatrix}(a_1+b_1)+c_1\\ \vdots \\ (a_n+b_n)+c_n\end{pmatrix} \\ &= \begin{pmatrix}a_1+(b_1+c_1)\\ \vdots \\ a_n+(b_n+c_n)\end{pmatrix} \\ &= \mathbf{a} + (\mathbf{b} + \mathbf{c}) \end{align} $$ より、成立します。

3. ベクトルのスカラー倍

(1) スカラーの定義

定義1.11: スカラー

スカラーとは、$1, 3+i$のようなベクトルではない1次元の普通の数を指す言葉で、ベクトルでないことを強調する際に用います。

$\alpha$をスカラーとした場合、$\alpha$が実数であれば$\alpha \in \mathbb{R}$、$\alpha$が複素数であれば$\alpha \in \mathbb{C}$と表記します。

(2) スカラー倍の定義

定義1.12: ベクトルのスカラー倍

スカラー $\lambda \in \mathbb{C}$ によるベクトル $\mathbf{a}=\begin{pmatrix}a_1 \\ \vdots \\ a_n \end{pmatrix} \in \mathbb{C}^n$ のスカラー倍は以下のように定義されます。 $$\lambda \mathbf{a} = \begin{pmatrix} \lambda a_1 \\ \vdots \\ \lambda a_n \end{pmatrix}$$

(3) スカラー倍の性質

結合法則(互換性)

$\alpha, \beta \in \mathbb{C}$と$\mathbf{a} \in \mathbb{C}^n$ について、以下が成立します。 $$ \alpha (\beta \mathbf{a}) = (\alpha \beta) \mathbf{a} $$

証明をみる

$\mathbf{a} = \begin{pmatrix}a_1 \\ \vdots \\ a_n\end{pmatrix}$とすると、 $$ \begin{align} \alpha (\beta \mathbf{a}) &= \alpha \begin{pmatrix} \beta a_1 \\ \vdots \\ \beta a_n \end{pmatrix}\\ &= \begin{pmatrix} \alpha\beta a_1 \\ \vdots \\ \alpha\beta a_n \end{pmatrix}\\ &= \begin{pmatrix} (\alpha\beta) a_1 \\ \vdots \\ (\alpha\beta) a_n \end{pmatrix}\\ &= (\alpha \beta) \mathbf{a} \end{align} $$ より成立します。

分配法則

$\alpha \in \mathbb{C}$と$\mathbf{a}, \mathbf{b} \in \mathbb{C}^n$について、以下が成立します。 $$\alpha(\mathbf{a} + \mathbf{b}) = \alpha \mathbf{a} + \alpha \mathbf{b}$$

証明をみる

$\mathbf{a} = \begin{pmatrix}a_1 \\ \vdots \\ a_n\end{pmatrix}$, $\mathbf{b} = \begin{pmatrix}b_1 \\ \vdots \\ b_n\end{pmatrix}$とすると、 $$ \begin{align} \alpha (\mathbf{a} + \mathbf{b}) &= \alpha \begin{pmatrix} a_1+b_1 \\ \vdots \\ a_n+b_n \end{pmatrix}\\ &= \begin{pmatrix} \alpha(a_1+b_1) \\ \vdots \\ \alpha(a_n+b_n) \end{pmatrix}\\ &= \begin{pmatrix} \alpha a_1 + \alpha b_1 \\ \vdots \\ \alpha a_n + \alpha b_n \end{pmatrix}\\ &= \begin{pmatrix} (\alpha a_1) + (\alpha b_1) \\ \vdots \\ (\alpha a_n) + (\alpha b_n) \end{pmatrix}\\ &= \alpha \mathbf{a} + \alpha \mathbf{b} \end{align} $$ より成立します。

4. ベクトルの内積とノルム

本節では実ベクトルの内積を扱います。複素ベクトルに拡張した内積については13章3節を参照して下さい。また、本節以降では縦ベクトル$\mathbf{a}=\begin{pmatrix}a_1 \\ \vdots \\ a_n\end{pmatrix} \in \mathbb{R}^n$の成分を横に並べた横ベクトル$\mathbf{a’} = (a_1, \cdots, a_n)$を、簡単のため$\mathbf{a’}=\mathbf{a}^T$と表記することにします。$\mathbf{a}^T$は$\mathbf{a}$の転置という概念であり、詳細については3章7節を参照して下さい。

(1) 内積の定義

定義1.13: 内積

$\mathbf{a} \in \mathbb{R}^n$と$\mathbf{b} \in \mathbb{R}^m$の内積は同じ次元、すなわち$n=m$の場合に定義され、$\mathbf{a}\cdot\mathbf{b}$と表記し、以下で定義されます。

$$ \mathbf{a}\cdot\mathbf{b} = \mathbf{a}^T\mathbf{b} $$

$\mathbf{a}^T\mathbf{b}$は、$\mathbf{a}=\begin{pmatrix}a_1 \\ \vdots \\ a_n\end{pmatrix}$, $\mathbf{b}=\begin{pmatrix}b_1 \\ \vdots \\ b_n\end{pmatrix}$とすると、以下で定義されます。

$$ \mathbf{a}^T\mathbf{b} = \sum_{i=1}^n a_ib_i $$

内積$\mathbf{a}\cdot\mathbf{b} = \mathbf{a}^T\mathbf{b}$は2つのベクトルからスカラーを与える演算であることに注意して下さい。また、$\mathbf{a}\cdot\mathbf{a}$を$\mathbf{a}^2$と表記することがあることにも注意して下さい。

(2) 内積の性質

交換法則

$\mathbf{a}, \mathbf{b} \in \mathbb{R}^n$について、以下が成立します。 $$ \mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a} $$

証明をみる

$\mathbf{a}, \mathbf{b}$の第$i$成分をそれぞれ$a_i, b_i$とすると、 $$ \begin{align} \mathbf{a} \cdot \mathbf{b} &= \mathbf{a}^T \mathbf{b} \\ &= \sum_i a_i b_i \\ &= \sum_i b_i a_i \\ &= \mathbf{b}^T \mathbf{a} \\ &= \mathbf{b} \cdot \mathbf{a} \end{align} $$

線形性

$\mathbf{a}, \mathbf{b}, \mathbf{c} \in \mathbb{R}^n$について、以下が成立します。 $$ \mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c} $$

証明をみる

$\mathbf{a}, \mathbf{b}, \mathbf{c}$の第$i$成分をそれぞれ$a_i, b_i, c_i$とすると、 $$ \begin{align} \mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) &= \mathbf{a}^T (\mathbf{b} + \mathbf{c}) \\ &= \sum_i a_i (b_i + c_i) \\ &= \sum_i a_i b_i + \sum_{i=1}^n a_i c_i \\ &= \mathbf{a}^T \mathbf{b} + \mathbf{a}^T \mathbf{c} \\ &= \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c} \end{align} $$

正値性

$\mathbf{a} \in \mathbb{R}^n$について、以下が成立します。 $$ \mathbf{a} \cdot \mathbf{a} \geq 0 $$

証明をみる

$\mathbf{a}$の第$i$成分を$a_i$とすると、 $$ \begin{align} \mathbf{a} \cdot \mathbf{a} &= \mathbf{a}^T \mathbf{a} \\ &= \sum_i a_i a_i\\ &= \sum_i a_i^2 \\ &\geq 0 \end{align} $$

(3) ノルムの定義

定義1.14: ノルム

$\mathbf{a} = \begin{pmatrix}a_1 \\ \vdots \\ a_n \end{pmatrix} \in \mathbb{R}^n$のノルムは$\|\mathbf{a}\|$と表記し、自身との内積の平方根で以下のように定義されます。なお、ノルムは長さや大きさとも呼ばれます。 $$ \|\mathbf{a}\| = \sqrt{\mathbf{a} \cdot \mathbf{a}} = \sqrt{\sum_{i=1}^n a_i^2} $$

(4) ノルムの性質

以下の性質があります。

ノルムの性質

$\lambda \in \mathbb{R}, \mathbf{a} \in \mathbb{R}^n$について、以下が成立します。

$\|\mathbf{a}\| \geq 0$
$\|\mathbf{a}\| = 0 \Leftrightarrow \mathbf{a} = \mathbf{0}$
$\|\lambda \mathbf{a}\| = |\lambda| \|\mathbf{a}\|$

証明は割愛します。

(5) 内積とノルムに関する定理(1)：単位ベクトル

定理1.15: 内積とノルムの関係

ゼロベクトルでない$\mathbf{a} \in \mathbb{R}^n$について、$\mathbf{a}/\|\mathbf{a}\|$は単位ベクトルとなります。

証明をみる

$\mathbf{a}/\|\mathbf{a}\|$のノルムが$1$であることを示せば十分です。$\|\mathbf{a}\|=n$とおくと、 $$ \begin{align} \Big\|\frac{\mathbf{a}}{\|\mathbf{a}\|}\Big\| &= \Big\|\frac{\mathbf{a}}{n}\Big\| \\ &= \frac{\|\mathbf{a}\|}{n} \\ &= \frac{n}{n} \\ &= 1 \end{align} $$ よって、題意成立となります。

(6) 内積とノルムに関する定理(2)：内積とノルムの関係

定理1.16: 内積とノルムの関係

$\mathbf{a}$と$\mathbf{b}$が2次元または3次元の実ベクトルであるとき、その2つのベクトルの成す角を$\theta$とすると、内積は以下にように表現できます。 $$ \mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\|\|\mathbf{b}\|\cos\theta $$

証明をみる

2次元平面または3次元空間上において、原点 $O$、点 $A$（位置ベクトル $\mathbf{a}$）、点 $B$（位置ベクトル $\mathbf{b}$）をとります。三角形 $OAB$ について、辺の長さは$OA=\|\mathbf{a}\|$、$OB=\|\mathbf{b}\|$、$AB=\|\mathbf{a}-\mathbf{b}\|$となります。また、$\angle AOB=\theta$ が $\mathbf{a}$ と $\mathbf{b}$ のなす角です。余弦定理より $$ \|\mathbf{a}-\mathbf{b}\|^2=\|\mathbf{a}\|^2+\|\mathbf{b}\|^2-2\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta $$ となります。一方、内積の性質から $$ \begin{align} \|\mathbf{a}-\mathbf{b}\|^2 &= (\mathbf{a}-\mathbf{b})\cdot(\mathbf{a}-\mathbf{b}) \\ &= \mathbf{a}\cdot\mathbf{a}+\mathbf{b}\cdot\mathbf{b}-2\mathbf{a}\cdot\mathbf{b} \\ &= \|\mathbf{a}\|^2+\|\mathbf{b}\|^2-2\mathbf{a}\cdot\mathbf{b} \end{align} $$ となります。従って、 $$ \|\mathbf{a}\|^2+\|\mathbf{b}\|^2-2\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|^2+\|\mathbf{b}\|^2-2\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta $$ 両辺から $\|\mathbf{a}\|^2+\|\mathbf{b}\|^2$ を消去して $-2$ で割ると $$ \mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\|\mathbf{b}\|\cos\theta $$ となります。以上より、題意成立となります。

(7) 内積とノルムに関する定理(3)：2つのベクトルが成す角度

定理1.17: 2つのベクトルが成す角度

$\mathbf{a}$と$\mathbf{b}$が2次元または3次元の実ベクトルであるとき、その2つのベクトルの成す角を$\theta$を以下のように求めることができます。 $$ \cos\theta = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \|\mathbf{b}\|} $$

証明をみる

内積とノルムの関係式を式変形することで得られます。

(8) 内積とノルムに関する定理(4)：直交の判定

定理1.18: 直交の判定

$\mathbf{a}$と$\mathbf{b}$が2次元または3次元の実ベクトルであるとき、「$\mathbf{a}$と$\mathbf{b}$が直交」と「$\mathbf{a}\cdot\mathbf{b}$」は同値です。

証明をみる

内積とノルムの関係式で$\theta=\pi/2$を代入することで証明できます。

(9) 内積とノルムに関する定理(5)：コーシー・シュワルツの不等式

定理1.19: 三角不等式

$\mathbf{a}, \mathbf{b} \in \mathbb{R}^n$について、以下が成立します。 $$ \mathbf{a} \cdot \mathbf{b} \leq \|\mathbf{a}\|\|\mathbf{b}\| $$

証明をみる

$t\in\mathbb{R}$について $$ \begin{align} \|\mathbf{a}-t\mathbf{b}\|^2 &= \|\mathbf{b}\|^2t^2 -2\mathbf{a}\cdot\mathbf{b}t + \|\mathbf{a}\|^2 \\ & \geq 0 \end{align} $$ となる。これは、$t$の2次式とみなした際の判別式が非正であることと同値なので、 $$ \begin{align} &(\mathbf{a}\cdot\mathbf{b})^2 – \|\mathbf{a}\|^2\|\mathbf{b}\|^2 \leq 0 \\ &\iff (\mathbf{a}\cdot\mathbf{b})^2 \leq \|\mathbf{a}\|^2\|\mathbf{b}\|^2 \\ &\iff (\mathbf{a}\cdot\mathbf{b}) \leq \|\mathbf{a}\|\|\mathbf{b}\| \end{align} $$ となります。以上より、題意成立となります。

※ 以下の関係式において$\cos \theta$が$-1$から$1$であることを用いる証明では、2次元または3次元ベクトルに対する証明にしかならないことに注意して下さい。 $$ \mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\|\|\mathbf{b}\|\cos\theta $$

(10) 内積とノルムに関する定理(6)：三角不等式

定理1.20: 2つのベクトルが成す角度

$\mathbf{a}, \mathbf{b} \in \mathbb{R}^n$について、以下が成立します。 $$ \|\mathbf{a} + \mathbf{b}\| \leq \|\mathbf{a}\| + \|\mathbf{b}\| $$

証明をみる

$$ \begin{align} (\|\mathbf{a}\| + \|\mathbf{b}\|)^2 = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2 + 2\|\mathbf{a}\|\|\mathbf{b}\| \end{align} $$ となります。ここで、コーシー・シュワルツの不等式を用いると、 $$ \begin{align} (\|\mathbf{a}\| + \|\mathbf{b}\|)^2 & = \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2 + 2\|\mathbf{a}\|\|\mathbf{b}\| \\ &\geq \|\mathbf{a}\|^2 + \|\mathbf{b}\|^2 + 2\mathbf{a}\cdot\mathbf{b} \\ &= (\mathbf{a} + \mathbf{b})^2 \end{align} $$ となります。従って、 $$ \begin{align} &(\|\mathbf{a}\| + \|\mathbf{b}\|)^2 \geq (\mathbf{a} + \mathbf{b})^2 \\ &\iff |\|\mathbf{a}\| + \|\mathbf{b}\|| \geq \|\mathbf{a} + \mathbf{b}\| \\ &\iff \|\mathbf{a}\| + \|\mathbf{b}\| \geq \|\mathbf{a} + \mathbf{b}\| \end{align} $$ となり、題意成立となります。

(11) 内積の公式 (1)

$\mathbf{a}, \mathbf{b} \in \mathbb{R}^n$について、以下が成立します。 $$ \mathbf{a} (\mathbf{a}^T\mathbf{b}) = (\mathbf{a}\mathbf{a}^T)\mathbf{b} $$

証明をみる

$\mathbf{a}$の第$i$成分を$a_i$とすると、 $$ \begin{align} (\mathbf{a}\mathbf{a}^T)\mathbf{b} &= \begin{pmatrix}a_1\mathbf{a}^T \\ \vdots \\ a_n\mathbf{a}^T\end{pmatrix}\mathbf{b} \\ &= \begin{pmatrix}a_1\mathbf{a}^T\mathbf{b} \\ \vdots \\ a_n\mathbf{a}^T\mathbf{b}\end{pmatrix} \\ &= \mathbf{a} (\mathbf{a}^T\mathbf{b}) \end{align} $$ となり、題意成立となります。

5. 外積

(1) 外積の定義

内積は2つのベクトルからスカラーを得る演算ですが、外積は2つのベクトルからベクトルを演算です。

定義1.18: 外積

$\mathbf{a}=(a_1, a_2, a_3)^T$と$\mathbf{b}=(b_1, b_2, b_3)^T$の外積$\mathbf{a} \times \mathbf{b}$は以下のように定義されます。 $$ \mathbf{a} \times \mathbf{b} = \begin{pmatrix} a_2 b_3 – a_3 b_2 \\ a_3 b_1 – a_1 b_3 \\ a_1 b_2 – a_2 b_1 \end{pmatrix} $$

(2) 外積の行列式による表現

行列式の余因子展開に倣ったベクトル値ラプラス展開(成分にベクトルが含まれる行列の余因子展開)を用いると、外積は以下のように表現できます。

行列式および余因子展開ならびにベクトル値ラプラス展開については以下の記事を参照して下さい。

$\mathbf{a}=(a_1, a_2, a_3)^T$, $\mathbf{b}=(b_1, b_2, b_3)^T$とし、また、$\mathbf{i}=(1, 0, 0)^T, \mathbf{j}=(0, 1, 0)^T, \mathbf{k}=(0, 0, 1)^T$とすると、 $$ \mathbf{a}\times\mathbf{b} =\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix} $$ と書けます。

証明をみる

ベクトルが1行目に含まれた行列の行列式は、ベクトル値ラプラス展開によって定義されます。具体的には、第1行目に関する余因子展開として以下のように定義されます。従って、 $$ \begin{align} \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix} &= (-1)^{1+1}\begin{vmatrix}a_2 & a_3 \\ b_2 & b_3\end{vmatrix}\mathbf{i} +(-1)^{1+2}\begin{vmatrix}a_1 & a_3 \\ b_1 & b_3\end{vmatrix}\mathbf{j} +(-1)^{1+3}\begin{vmatrix}a_1 & a_2 \\ b_1 & b_2\end{vmatrix}\mathbf{k} \\ &= (a_2b_3 – a_3b_2)\mathbf{i} – (a_1b_3 – a_3b_1)\mathbf{j} + (a_1b_2 – a_2b_1)\mathbf{k} \\ &= \begin{pmatrix}a_2b_3 – a_3b_2 \\ a_3b_1 – a_1b_3 \\ a_1b_2 – a_2b_1\end{pmatrix} \end{align} $$ となり、題意成立となります。

(3) 外積の行列による表現

外積は行列とベクトルの積としても表現できます。

ベクトル $\mathbf{a}=(a_1,a_2,a_3)^{\mathsf T} \in \mathbb{R}^3$ に対し，クロス積行列（反対称行列） $$ [\mathbf{a}]_\times=\begin{pmatrix} 0&-a_3&a_2\\ a_3&0&-a_1\\ -a_2&a_1&0 \end{pmatrix} $$ を定めると，任意の $\mathbf{b}\in\mathbb{R}^3$ に対して $$ \mathbf{a}\times\mathbf{b}=[\mathbf{a}]_\times\,\mathbf{b} $$ が成り立ちます。

証明をみる

(4) 外積の性質

外積は以下の性質を満たします。いずれも成分を用いて証明ができます。

反交換法則

$$\mathbf{a} \times \mathbf{b} = -(\mathbf{b} \times \mathbf{a})$$

証明をみる

外積は $$ \mathbf{a}\times\mathbf{b} =\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix} $$ と書けます。ここで第2行と第3行$(\mathbf{a}$ と $\mathbf{b}$）を交換すると行列式は符号が反転するので $$ \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ b_1 & b_2 & b_3\\ a_1 & a_2 & a_3 \end{vmatrix} =-(\mathbf{a}\times\mathbf{b}) $$ ですが、左辺はまさに $\mathbf{b}\times\mathbf{a}$ です。したがって $$ \boxed{\ \mathbf{a}\times\mathbf{b}=-(\mathbf{b}\times\mathbf{a})\ }. $$ 行列式については以下の記事を参照。

分配法則

$$\mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c}$$

証明をみる

外積は形式的に $$ \mathbf{a}\times\mathbf{b} =\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix} $$ と書ける。第3行に関して行列式は線形なので $$ \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1+c_1 & b_2+c_2 & b_3+c_3 \end{vmatrix} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix} + \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ c_1 & c_2 & c_3 \end{vmatrix} =\mathbf{a}\times\mathbf{b}+\mathbf{a}\times\mathbf{c}. $$ したがって所望の分配法則が成り立つ。
行列式については以下の記事を参照。

結合法則

$$(\lambda \mathbf{a}) \times \mathbf{b} = \lambda (\mathbf{a} \times \mathbf{b})$$

証明をみる

外積は形式的に $$ \mathbf{a}\times\mathbf{b} =\begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix} $$ と書ける。第2行（$\mathbf{a}$ の行）に関して行列式は線形なので $$ \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ \lambda a_1 & \lambda a_2 & \lambda a_3\\ b_1 & b_2 & b_3 \end{vmatrix} =\lambda \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k}\\ a_1 & a_2 & a_3\\ b_1 & b_2 & b_3 \end{vmatrix} =\lambda(\mathbf{a}\times\mathbf{b}). $$ したがって $$ \boxed{\,(\lambda \mathbf{a}) \times \mathbf{b} = \lambda (\mathbf{a} \times \mathbf{b})\,}. $$ 行列式については以下の記事を参照。

(5) 外積の公式 (1)：スカラー三重積

(6) 外積の公式 (2)：スカラー三重積の巡回対称性

(7) 外積の公式 (3)：ベクトル三重積

(8) 外積の公式 (4)：外積の恒等式

$$ (\mathbf{a} \times \mathbf{b}) \cdot (\mathbf{x} \times \mathbf{y}) $$

(9) 外積の公式 (5)：行列の恒等式

(10) 外積の公式 (6)：ラグランジュの恒等式

(11) 外積の向き

(12) 外積のノルム

(3) 外積に関する定理(1)：行列式を用いた表現

定理1.19: 外積の行列式による表現

証明をみる

第1行目の余因子展開より明らか。
余因子展開の詳しい説明については以下の記事を参照。

(4) 外積に関する定理(2)：外積の向き

定理:1.20: 外積の向き

$\mathbf{a} \times \mathbf{b}$の方向は$\mathbf{a}$を$\mathbf{b}$へ重ねるように右ねじを回した際の方向です (回す角度は$\pi$以下)。外積は$\mathbf{a}$と$\mathbf{b}$が含まれる平面に垂直な方向になります。

証明をみる (成分計算による証明)

$\mathbf{a}=(a_1,a_2,a_3)^{\mathsf T}$、$\mathbf{b}=(b_1,b_2,b_3)^{\mathsf T}$ とする。外積の成分は $$ \mathbf{a}\times\mathbf{b}=\bigl(a_2b_3-a_3b_2,\ a_3b_1-a_1b_3,\ a_1b_2-a_2b_1\bigr)^{\mathsf T} $$ まず、(1)$\mathbf{a}\cdot(\mathbf{a}\times\mathbf{b})=0$ を示す。左辺を成分で展開すると $$ \mathbf{a}\cdot(\mathbf{a}\times\mathbf{b})=a_1(a_2b_3-a_3b_2)+a_2(a_3b_1-a_1b_3)+a_3(a_1b_2-a_2b_1) $$ 項を並べ替えて同類項をまとめると $$ =a_1a_2b_3-a_1a_3b_2+a_2a_3b_1-a_1a_2b_3+a_1a_3b_2-a_2a_3b_1=0 $$ 相殺してすべて消えるため $0$ である。
続いて (2)$\mathbf{b}\cdot(\mathbf{a}\times\mathbf{b})=0$ を示す。
同様に $$ \mathbf{b}\cdot(\mathbf{a}\times\mathbf{b})=b_1(a_2b_3-a_3b_2)+b_2(a_3b_1-a_1b_3)+b_3(a_1b_2-a_2b_1) $$ これを展開すると $$ =a_2b_1b_3-a_3b_1b_2+a_3b_1b_2-a_1b_2b_3+a_1b_2b_3-a_2b_1b_3=0 $$ やはりすべての項が打ち消し合って $0$ となる。
(1)(2)より $$ \mathbf{a}\cdot(\mathbf{a}\times\mathbf{b})=0,\quad \mathbf{b}\cdot(\mathbf{a}\times\mathbf{b})=0 $$ したがって $\mathbf{a}\times\mathbf{b}$ は $\mathbf{a}$ と $\mathbf{b}$ の両方に直交する。

証明をみる (行列式を用いた証明)

スカラー三重積の性質を用いると $$ \mathbf{a}\cdot(\mathbf{a}\times\mathbf{b})=\det[\mathbf{a},\mathbf{a},\mathbf{b}] $$ となる。行列式は列（または行）が同一なら $0$ なので $$ \det[\mathbf{a},\mathbf{a},\mathbf{b}]=0 $$ 同様に $$ \mathbf{b}\cdot(\mathbf{a}\times\mathbf{b})=\det[\mathbf{b},\mathbf{a},\mathbf{b}]=0 $$ よって直交性がただちに従う。
行列の積については以下の記事を参照。

行列式については以下の記事を参照。

(5) 外積に関する定理(3)：外積のノルム

定理1.21: 外積のノルム

外積のノルムは以下です。 $$|\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| |\mathbf{b}| \sin \theta$$ 外積の大きさは$\mathbf{a}$と$\mathbf{b}$が作る平行四辺形の面積に相当します。

証明をみる

次の恒等式（ラグランジュの恒等式）を用いる： $$ \|\mathbf{a}\times\mathbf{b}\|^2=\|\mathbf{a}\|^2\|\mathbf{b}\|^2-(\mathbf{a}\cdot\mathbf{b})^2 $$ この式は外積の成分定義から直接展開しても示せるし、行列式の恒等式としても知られている。証明は本証明の最後に導出を載せた。
内積の基本公式 $\mathbf{a}\cdot\mathbf{b}=\|\mathbf{a}\|\,\|\mathbf{b}\|\cos\theta$ を代入すると $$ \|\mathbf{a}\times\mathbf{b}\|^2=\|\mathbf{a}\|^2\|\mathbf{b}\|^2-\big(\|\mathbf{a}\|\,\|\mathbf{b}\|\cos\theta\big)^2 $$ $$ \|\mathbf{a}\times\mathbf{b}\|^2=\|\mathbf{a}\|^2\|\mathbf{b}\|^2\big(1-\cos^2\theta\big)=\|\mathbf{a}\|^2\|\mathbf{b}\|^2\sin^2\theta $$ 両辺は非負なので平方根を取って $$ \|\mathbf{a}\times\mathbf{b}\|=\|\mathbf{a}\|\,\|\mathbf{b}\|\sin\theta $$ が得られる。□

ラグランジュの恒等式の導出 (成分を用いた証明)

$\|\mathbf{a}\times\mathbf{b}\|^2=(\mathbf{a}\times\mathbf{b})\cdot(\mathbf{a}\times\mathbf{b})$ を展開すると $(\mathbf{a}\cdot\mathbf{a})(\mathbf{b}\cdot\mathbf{b})-(\mathbf{a}\cdot\mathbf{b})^2$ になる。これは成分展開またはベクトル恒等式 $(\mathbf{u}\times\mathbf{v})\cdot(\mathbf{x}\times\mathbf{y})=(\mathbf{u}\cdot\mathbf{x})(\mathbf{v}\cdot\mathbf{y})-(\mathbf{u}\cdot\mathbf{y})(\mathbf{v}\cdot\mathbf{x})$ の特殊化で示せる。

成分展開による証明は以下。
まず、$\mathbf{a}=(a_1,a_2,a_3),\ \mathbf{b}=(b_1,b_2,b_3)$とおく。
(1) 左辺の成分展開
外積の成分は $$ \mathbf{a}\times\mathbf{b}=(a_2b_3-a_3b_2,\ a_3b_1-a_1b_3,\ a_1b_2-a_2b_1). $$ よってノルム二乗は $$ \|\mathbf{a}\times\mathbf{b}\|^2=(a_2b_3-a_3b_2)^2+(a_3b_1-a_1b_3)^2+(a_1b_2-a_2b_1)^2. $$ 各項を展開して和をとると $$ \begin{aligned} \|\mathbf{a}\times\mathbf{b}\|^2 &=(a_2^2b_3^2+a_3^2b_2^2-2a_2a_3b_2b_3)\\ &\quad+(a_3^2b_1^2+a_1^2b_3^2-2a_3a_1b_3b_1)\\ &\quad+(a_1^2b_2^2+a_2^2b_1^2-2a_1a_2b_1b_2)\\ &=a_1^2(b_2^2+b_3^2)+a_2^2(b_3^2+b_1^2)+a_3^2(b_1^2+b_2^2)\\ &\quad-2(a_1a_2b_1b_2+a_2a_3b_2b_3+a_3a_1b_3b_1). \end{aligned} $$ (2) 右辺の成分展開
まず $$ \|\mathbf{a}\|^2\|\mathbf{b}\|^2=(a_1^2+a_2^2+a_3^2)(b_1^2+b_2^2+b_3^2). $$ 展開すると $$ \begin{aligned} \|\mathbf{a}\|^2\|\mathbf{b}\|^2 &=a_1^2(b_1^2+b_2^2+b_3^2)+a_2^2(b_1^2+b_2^2+b_3^2)+a_3^2(b_1^2+b_2^2+b_3^2)\\ &=a_1^2b_1^2+a_1^2b_2^2+a_1^2b_3^2+a_2^2b_1^2+a_2^2b_2^2+a_2^2b_3^2+a_3^2b_1^2+a_3^2b_2^2+a_3^2b_3^2. \end{aligned} $$ 次に $$ (\mathbf{a}\cdot\mathbf{b})^2=(a_1b_1+a_2b_2+a_3b_3)^2 =a_1^2b_1^2+a_2^2b_2^2+a_3^2b_3^2+2(a_1a_2b_1b_2+a_2a_3b_2b_3+a_3a_1b_3b_1). $$ したがって差は $$ \begin{aligned} \|\mathbf{a}\|^2\|\mathbf{b}\|^2-(\mathbf{a}\cdot\mathbf{b})^2 &=\big[a_1^2(b_1^2+b_2^2+b_3^2)+a_2^2(b_1^2+b_2^2+b_3^2)+a_3^2(b_1^2+b_2^2+b_3^2)\big]\\ &\quad-\big[a_1^2b_1^2+a_2^2b_2^2+a_3^2b_3^2+2(a_1a_2b_1b_2+a_2a_3b_2b_3+a_3a_1b_3b_1)\big]\\ &=a_1^2(b_2^2+b_3^2)+a_2^2(b_1^2+b_3^2)+a_3^2(b_1^2+b_2^2)\\ &\quad-2(a_1a_2b_1b_2+a_2a_3b_2b_3+a_3a_1b_3b_1). \end{aligned} $$ (3) 一致の確認と結論
1) の結果と 2) の最後の式は項ごとに一致する。したがって $$ \|\mathbf{a}\times\mathbf{b}\|^2=\|\mathbf{a}\|^2\|\mathbf{b}\|^2-(\mathbf{a}\cdot\mathbf{b})^2 $$ が成り立つ。これがラグランジュの恒等式の成分計算による証明である。□

ラグランジュの恒等式の導出 (反対称行列（クロス積行列）を用いる証明)

ベクトル $\mathbf{a}=(a_1,a_2,a_3)^{\mathsf T}$ に対し，クロス積行列（反対称行列） $$ [\mathbf{a}]_\times=\begin{pmatrix} 0&-a_3&a_2\\ a_3&0&-a_1\\ -a_2&a_1&0 \end{pmatrix} $$ を定めると，任意の $\mathbf{b}\in\mathbb{R}^3$ に対して $$ \mathbf{a}\times\mathbf{b}=[\mathbf{a}]_\times\,\mathbf{b} $$ が成り立つ。まず重要な行列恒等式を示す： $$ [\mathbf{a}]_\times^{\mathsf T}[\mathbf{a}]_\times=(\mathbf{a}\cdot\mathbf{a})I-\mathbf{a}\mathbf{a}^{\mathsf T}. $$ これはベクトル三重積の公式 $\mathbf{a}\times(\mathbf{a}\times\mathbf{x})=\mathbf{a}(\mathbf{a}\cdot\mathbf{x})-\mathbf{x}(\mathbf{a}\cdot\mathbf{a})$ を行列形で書くと $$ [\mathbf{a}]_\times^2=\mathbf{a}\mathbf{a}^{\mathsf T}-(\mathbf{a}\cdot\mathbf{a})I $$ となることから，$[\mathbf{a}]_\times^{\mathsf T}=-[\mathbf{a}]_\times$ を用いて $$ [\mathbf{a}]_\times^{\mathsf T}[\mathbf{a}]_\times=-[\mathbf{a}]_\times^2=(\mathbf{a}\cdot\mathbf{a})I-\mathbf{a}\mathbf{a}^{\mathsf T} $$ が従う。これで $$ \|\mathbf{a}\times\mathbf{b}\|^2=(\mathbf{a}\times\mathbf{b})\cdot(\mathbf{a}\times\mathbf{b})=\big([\mathbf{a}]_\times\mathbf{b}\big)^{\mathsf T}\big([\mathbf{a}]_\times\mathbf{b}\big)=\mathbf{b}^{\mathsf T}\big([\mathbf{a}]_\times^{\mathsf T}[\mathbf{a}]_\times\big)\mathbf{b} $$ $$ =\mathbf{b}^{\mathsf T}\big((\mathbf{a}\cdot\mathbf{a})I-\mathbf{a}\mathbf{a}^{\mathsf T}\big)\mathbf{b}=(\mathbf{a}\cdot\mathbf{a})(\mathbf{b}\cdot\mathbf{b})-(\mathbf{a}\cdot\mathbf{b})^2 $$ となり，求める恒等式が得られる。□
行列の積については以下の記事を参照。

(6) 外積に関する定理(4)：スカラー三重積

定理1.22: スカラー三重積（混合積）

3つのベクトル $\mathbf{a}, \mathbf{b}, \mathbf{c}$ に対して、以下をスカラー三重積（または混合積）という。 $$\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c})$$ スカラー三重積はスカラーであり、幾何学的には $\mathbf{a}, \mathbf{b}, \mathbf{c}$ によって張られる平行六面体の符号付き体積を表す。

証明をみる (幾何学的証明)

外積の大きさと方向より $$ |\mathbf{b}\times\mathbf{c}|=|\mathbf{b}|\,|\mathbf{c}|\,\sin\theta $$ $(\theta$ は $\mathbf{b},\mathbf{c}$ のなす角であり、$\mathbf{b}\times\mathbf{c}$ は $\mathbf{b},\mathbf{c}$ に直交し、右手系で向きが定まる。ゆえに $$ \mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) =|\mathbf{a}|\,|\mathbf{b}\times\mathbf{c}|\,\cos\varphi $$ $(\varphi$ は $\mathbf{a}$ と $\mathbf{b}\times\mathbf{c}$ のなす角）。ここで $$ |\mathbf{b}\times\mathbf{c}| \ \text{は底面（$\mathbf{b},\mathbf{c}$）の面積},\qquad |\mathbf{a}|\,\cos\varphi = \operatorname{proj}_{\mathbf{n}}(\mathbf{a}) $$ （$\mathbf{n}$ は $\mathbf{b}\times\mathbf{c}$ 方向の単位ベクトル）に等しいので、 $$ |\mathbf{a}|\,\cos\varphi \cdot |\mathbf{b}\times\mathbf{c}|=\text{底面積}\times\text{高さ}=\text{体積}. $$ また符号は、$\{\mathbf{a},\mathbf{b},\mathbf{c}\}$ が右手系（正の向き）なら正、左手系（負の向き）なら負として与えられる。したがって $$ \mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) $$ は平行六面体の**符号付き体積**を与える。

証明をみる (行列式を用いた証明)

標準基底に関する成分を $\mathbf{a}=(a_1,a_2,a_3),\ \mathbf{b}=(b_1,b_2,b_3),\ \mathbf{c}=(c_1,c_2,c_3)$ とすると $$ \mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) = \begin{vmatrix} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 & c_3 \end{vmatrix} =:\det[\mathbf{a},\mathbf{b},\mathbf{c}]. $$ 行列式は、3本のベクトルから張られる平行六面体の体積の**符号付き**版（3線形性・交代性・単位立方体で値1）を特徴づける唯一の関数である。よって $$ \mathbf{a}\cdot(\mathbf{b}\times\mathbf{c})=\det[\mathbf{a},\mathbf{b},\mathbf{c}] $$ は平行六面体の符号付き体積に等しい。
行列式については以下の記事を参照。

(7) 外積に関する定理(5)：スカラー三重積の巡回対称性

定理1.23: スカラー三重積（混合積）の巡回対称性

以下の性質が成り立ちます。 $\mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \mathbf{b} \cdot (\mathbf{c} \times \mathbf{a}) = \mathbf{c} \cdot (\mathbf{a} \times \mathbf{b})$

証明をみる

\[ \mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) = \begin{vmatrix} a_1 & a_2 & a_3\\ b_1 & b_2 & b_3\\ c_1 & c_2 & c_3 \end{vmatrix}. \] 行列の行を $(1,2,3)\to(2,3,1)$ や $(1,2,3)\to(3,1,2)$ と巡回する操作は 3-巡回置換であり、これは偶置換なので行列式の値は不変。したがって \[ \begin{vmatrix} a\\ b\\ c \end{vmatrix} = \begin{vmatrix} b\\ c\\ a \end{vmatrix} = \begin{vmatrix} c\\ a\\ b \end{vmatrix}, \] すなわち $ \mathbf{a}\cdot(\mathbf{b}\times\mathbf{c}) = \mathbf{b}\cdot(\mathbf{c}\times\mathbf{a}) = \mathbf{c}\cdot(\mathbf{a}\times\mathbf{b}) $。
行列式については以下の記事を参照。

(8) 外積に関する定理(6)：ベクトル三重積

定理1.24: ベクトル三重積

以下をベクトル三重積という。 $$\mathbf{a} \times (\mathbf{b} \times \mathbf{c})$$ ベクトル三重積はベクトルであり、以下の性質が成り立つ。 $$\mathbf{a} \times (\mathbf{b} \times \mathbf{c}) = (\mathbf{a} \cdot \mathbf{c})\mathbf{b} – (\mathbf{a} \cdot \mathbf{b})\mathbf{c}$$

証明をみる

ベクトル $\mathbf{a}=(a_1,a_2,a_3)$，$\mathbf{b}=(b_1,b_2,b_3)$，$\mathbf{c}=(c_1,c_2,c_3)$ とする。
まず $\mathbf{b}\times\mathbf{c}$ の成分は外積の定義より $$ \mathbf{b}\times\mathbf{c}= \begin{pmatrix} b_2c_3-b_3c_2\\ b_3c_1-b_1c_3\\ b_1c_2-b_2c_1 \end{pmatrix} $$ である。
次に，$\mathbf{a}\times(\mathbf{b}\times\mathbf{c})$ を計算する： $$ \mathbf{a}\times(\mathbf{b}\times\mathbf{c}) =\begin{pmatrix} a_2(b_1c_2-b_2c_1)-a_3(b_3c_1-b_1c_3)\\ a_3(b_2c_3-b_3c_2)-a_1(b_1c_3-b_3c_1)\\ a_1(b_3c_1-b_1c_3)-a_2(b_2c_1-b_1c_2) \end{pmatrix}. $$ 各成分を整理する。
(1) 第1成分：
$$ a_2(b_1c_2-b_2c_1)-a_3(b_3c_1-b_1c_3) =a_2b_1c_2-a_2b_2c_1-a_3b_3c_1+a_3b_1c_3. $$ これを $(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c}$ の第1成分と比較する。 – $(\mathbf{a}\cdot\mathbf{c})=a_1c_1+a_2c_2+a_3c_3$
– $(\mathbf{a}\cdot\mathbf{b})=a_1b_1+a_2b_2+a_3b_3$
したがって，第1成分は $$ (\mathbf{a}\cdot\mathbf{c})b_1-(\mathbf{a}\cdot\mathbf{b})c_1 = b_1(a_1c_1+a_2c_2+a_3c_3)-c_1(a_1b_1+a_2b_2+a_3b_3) $$ $$ = a_2b_1c_2+a_3b_1c_3 – a_2b_2c_1 – a_3b_3c_1, $$ これは上で計算した第1成分と一致する。
(2) 第2成分：
同様に計算すると $$ a_3b_2c_3-a_3b_3c_2-a_1b_1c_3+a_1b_3c_1 $$ となる。
一方，式 $(\mathbf{a}\cdot\mathbf{c})b_2-(\mathbf{a}\cdot\mathbf{b})c_2$ の第2成分は $$ b_2(a_1c_1+a_2c_2+a_3c_3)-c_2(a_1b_1+a_2b_2+a_3b_3) $$ $$ = a_3b_2c_3+a_1b_2c_1 – a_1b_1c_2 – a_3b_3c_2. $$ これも一致する。
(3) 第3成分：
同様に計算すると $$ a_1b_3c_1-a_1b_1c_3-a_2b_2c_1+a_2b_1c_2 $$ となる。
一方，式 $(\mathbf{a}\cdot\mathbf{c})b_3-(\mathbf{a}\cdot\mathbf{b})c_3$ の第3成分は $$ b_3(a_1c_1+a_2c_2+a_3c_3)-c_3(a_1b_1+a_2b_2+a_3b_3) $$ $$ = a_1b_3c_1+a_2b_3c_2 – a_1b_1c_3 – a_2b_2c_3, $$ これも一致する。 (1)(2)(3)より3つの成分が全て一致するので $$ \mathbf{a}\times(\mathbf{b}\times\mathbf{c})=(\mathbf{a}\cdot\mathbf{c})\mathbf{b}-(\mathbf{a}\cdot\mathbf{b})\mathbf{c} $$ が成り立つ。□

(9) まとめ

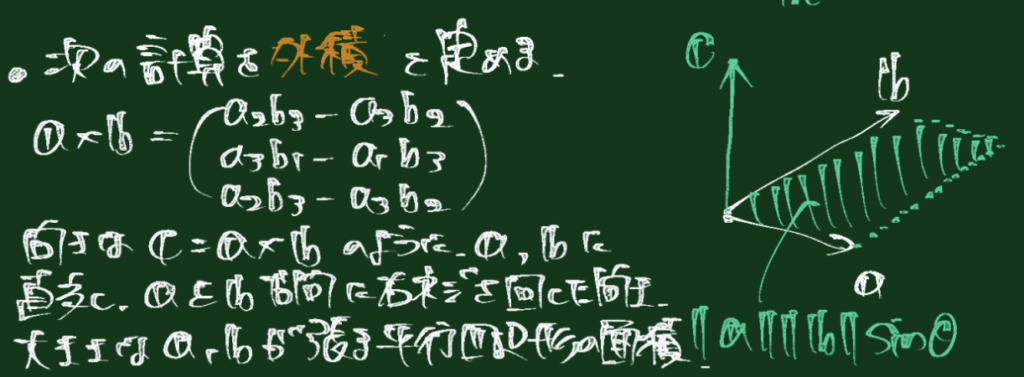
7. 1次独立と1次従属

(1) 1次独立

定義1.25: 1次独立

ベクトル $\mathbf{a}_1, \mathbf{a}_2, \dots, \mathbf{a}_k$ が 1次独立であるとは、以下の線形結合がゼロベクトルになるとき、すべての係数が 0 に限ることを言います。 $$c_1 \mathbf{a}_1 + c_2 \mathbf{a}_2 + \cdots + c_k \mathbf{a}_k = \mathbf{0} \Rightarrow c_1 = c_2 = \cdots = c_k = 0$$ すなわち、ベクトル同士が互いに冗長でなく、それぞれが独立した方向を持つこと(=どんな2つのベクトルも平行ではないこと)を意味します。

なお、2つのベクトルが1次独立の場合、$\mathbf{a} /\!/\!\!\!\!\backslash\, \mathbf{b}$と表記することがあります。

(2) 1次従属

定義1.26: 1次従属

ベクトル $\mathbf{a}_1, \mathbf{a}_2, \dots, \mathbf{a}_k$ が 1次従属であるとは、ゼロでない係数を用いた線形結合がゼロベクトルになる場合です。 $$c_1 \mathbf{a}_1 + c_2 \mathbf{a}_2 + \cdots + c_k \mathbf{a}_k = \mathbf{0}, \quad \text{ただし } \exists i \text{ such that } c_i \neq 0$$ つまり、少なくとも1つのベクトルが他のベクトルの線形結合として表されることを意味します。

なお、2つのベクトルが1次独立の場合、$\mathbf{a} /\!/ \mathbf{b}$と表記することがあります。