- 1. 行列の定義
- 2. 行列の和
- 3. 行列のスカラー倍
- 4. 行列の積
- (1) 行列の積の定義
- (2) 行列の積の定義の背景
- (3) 行列の積の性質(1)
- (4) 行列の積の性質(2)：ブロックに分けて計算
- (5) 様々な行列(4)：単位行列
- (6) 様々な行列(5)：ゼロ行列
- (7) 様々な行列(6)：ゼロ因子
- (8) 様々な行列(7)：べき零行列（ニルポテント）
- (9) 様々な行列(8)：べき等行列（イドポテント）
- (10) 行列の積に関する定理(1)：$a\mathbf{x}+b\mathbf{y}+c\mathbf{z}$の分解
- (11) 行列の積に関する定理(2)：$(a\mathbf{x},\,b\mathbf{y},\,c\mathbf{z})$の分解
- (12) 行列の積に関する定理(3)： $(a\mathbf{x},\,\mathbf{x}+b\mathbf{y},\,\mathbf{y}+c\mathbf{z})$の分解
- (13) 行列の積に関する定理(4)：対角行列の積
- (14) 行列の積に関する定理(5)：三角行列の積
- (13) まとめ
- 5. 行列式
- 6. 逆行列
- 7. 転置
- 8. トレース
1. 行列の定義
(1) 行列の定義
定義3.1: 行列
行列はベクトルを並べたものです。$m$ 行 $n$ 列の行列は $m$ 本の行ベクトル（または $n$ 本の列ベクトル）を長方形に並べたもので，
$$
A = (a_{ij})=
\begin{pmatrix}
a_{11} & a_{12} & \dots & a_{1n} \\
a_{21} & a_{22} & \dots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \dots & a_{mn}
\end{pmatrix}
$$
と書きます。各 $a_{ij}$ を 成分 といいます。
行は横方向の並びのことで$i$ 行目は $(a_{i1},\dots,a_{in})$です。また、列は縦方向の並びのことで$j$ 列目は $\begin{pmatrix} a_{1j} \ \vdots, \ a_{mj} \end{pmatrix}$です。行と列を混同しないように注意して下さい。
なお、以降はベクトルを行列の特殊な場合とみなします。すなわち、行ベクトルは 1 行だけを持つ $1\times n$ 行列：$\displaystyle \mathbf{y}=\begin{pmatrix}y_1&\dots&y_n\end{pmatrix}$、列ベクトルは 1 列だけを持つ $m\times 1$ 行列：$\displaystyle \mathbf{x}=\begin{pmatrix}x_1\\ \vdots\\ x_m\end{pmatrix}$とみなします。行ベクトルはと列ベクトルについては以下の記事も参照して下さい。
(2) 様々な行列(1)：正方行列
定義3.2: 正方行列
行と列の数が等しい $n\times n$ 行列を 正方行列 といいます。
(3) 様々な行列(2)：対角行列
定義3.3: 対角行列
非対角成分(=$a_{ii}$成分)がすべて $0$ の正方行列を対角行列といいます。
$$
\mathrm{diag}(d_1,\dots,d_n)=
\begin{pmatrix}
d_1 & 0 & \dots & 0\\
0 & d_2 & \dots & 0\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \dots & d_n
\end{pmatrix}.
$$
(4) 様々な行列(3)：三角行列
定義3.4: 三角行列
対角成分より下が $0$の行列を上三角行列といいます。対角成分より上が $0$の行列を下三角行列といいます。
2. 行列の和
(1) 行列の和と差の定義
定義3.5: 行列の和
$A,B$ が同じサイズ $m\times n$ のときのみ $A\pm B$ が定義され、成分同士の和または差$(A\pm B)_{ij}=a_{ij}\pm b_{ij}$で与えられます。
(2) 行列の和と差の性質
交換法則
$A+B=B+A$
証明をみる
成分ごとに $a_{ij}+b_{ij}=b_{ij}+a_{ij}$（実数の交換法則）より成り立つ。結合法則
$(A+B)+C=A+(B+C)$
証明をみる
$((A+B)+C)_{ij}=(a_{ij}+b_{ij})+c_{ij}=a_{ij}+(b_{ij}+c_{ij})=(A+(B+C))_{ij}$（実数の結合法則）。よって両辺の全成分が一致。$\square$3. 行列のスカラー倍
(1) 行列のスカラー倍の定義
定義3.6: 行列のスカラー倍
スカラー$\alpha \in \mathbb{C}$は成分のスカラー倍、すなわち以下で定義されます。
$$(\alpha A)_{ij}=\alpha a_{ij}$$
(2) 行列のスカラー倍の性質
線形性(1)
$(\alpha+\beta)A=\alpha A+\beta A$
証明をみる
$((\alpha+\beta)A)_{ij}=(\alpha+\beta)a_{ij}=\alpha a_{ij}+\beta a_{ij}=(\alpha A+\beta A)_{ij}$。線形性(2)
$\alpha(A+B)=\alpha A+\alpha B$
証明をみる
左辺 $(\alpha(A+B))_{ij}=\alpha(a_{ij}+b_{ij})=\alpha a_{ij}+\alpha b_{ij}=(\alpha A+\alpha B)_{ij}$。$\square$4. 行列の積
(1) 行列の積の定義
定義3.7: 行列の積
行列$A, B$の積$AB$は$A$の列数と$B$の行数が等しいときのみ定義されます。
具体的には、$m\times n$ 行列 $A=(a_{ik})$ と $n\times p$ 行列 $B=(b_{kj})$ の積 $C=AB$ は $m\times p$ 行列で以下で与えられます。
$$c_{ij}=\sum_{k=1}^n a_{ik}b_{kj}.$$
(2) 行列の積の定義の背景
線形写像の合成に矛盾が生じないように行列の積が定義されています。
定理3.8: 行列の積と線形写像の関係
線形写像 $T:\mathbb{R}^n\to\mathbb{R}^m$，$S:\mathbb{R}^p\to\mathbb{R}^n$ の合成 $T\circ S:\mathbb{R}^p\to\mathbb{R}^m$ に対し，標準基底に関する行列表現を $A,B$ とすると，合成の行列は $AB$ になります。すなわち，任意のベクトル $\mathbf{x}\in\mathbb{R}^p$ について
$$T(S(\mathbf{x}))=A(B\mathbf{x})=(AB)\mathbf{x},$$
線形写像については以下の記事を参照して下さい。
証明をみる (成分を用いた証明)
行列 $A$ を $m\times n$、行列 $B$ を $n\times p$ とし、積 $C=AB$ は $m\times p$ 行列とする。線形写像の合成式 $$ A(B\mathbf{x})=(AB)\mathbf{x} $$ を用いて、$C$ の成分 $c_{ij}$ が $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj} $$ で与えられることを示す。$\mathbf{x}\in\mathbb{R}^p$ を任意の列ベクトルとする。まず $B\mathbf{x}$ の第 $k$ 成分は $$ (B\mathbf{x})_k=\sum_{j=1}^{p}b_{kj}x_j. $$ 次に $A(B\mathbf{x})$ の第 $i$ 成分は $$ \bigl(A(B\mathbf{x})\bigr)_i=\sum_{k=1}^{n}a_{ik}(B\mathbf{x})_k=\sum_{k=1}^{n}a_{ik}\left(\sum_{j=1}^{p}b_{kj}x_j\right)=\sum_{j=1}^{p}\left(\sum_{k=1}^{n}a_{ik}b_{kj}\right)x_j. $$ 一方で、$C=AB$ とおいたとき $(C\mathbf{x})_i$ は $$ (C\mathbf{x})_i=\sum_{j=1}^{p}c_{ij}x_j. $$ 合成の等式 $A(B\mathbf{x})=(AB)\mathbf{x}=C\mathbf{x}$ より、任意の $\mathbf{x}$ に対して $$ \sum_{j=1}^{p}\left(\sum_{k=1}^{n}a_{ik}b_{kj}\right)x_j=\sum_{j=1}^{p}c_{ij}x_j $$ が成り立つ。これは全ての $x_j$ に対して成り立つ恒等式なので、各係数が一致しなければならない。ゆえに $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj}\qquad(1\le i\le m,\ 1\le j\le p). $$
証明をみる (標準基底ベクトルの像を用いる証明)
行列 $A$ を $m\times n$、行列 $B$ を $n\times p$ とし、積 $C=AB$ は $m\times p$ 行列とする。線形写像の合成式 $$ A(B\mathbf{x})=(AB)\mathbf{x} $$ を用いて、$C$ の成分 $c_{ij}$ が $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj} $$ で与えられることを示す。$\mathbf{e}_j\in\mathbb{R}^p$ を第 $j$ 成分のみ $1$、他は $0$ の標準基底とする。$B\mathbf{e}_j$ は $B$ の第 $j$ 列で、その第 $k$ 成分は $b_{kj}$ である。よって $$ A(B\mathbf{e}_j)=A\begin{pmatrix}b_{1j}\\ \vdots\\ b_{nj}\end{pmatrix} $$ の第 $i$ 成分は $$ \sum_{k=1}^{n}a_{ik}b_{kj}. $$ 一方、$A(B\mathbf{e}_j)=(AB)\mathbf{e}_j=C\mathbf{e}_j$ は $C$ の第 $j$ 列であり、その第 $i$ 成分は $c_{ij}$。したがって $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj}. $$ 以上で、線形写像の合成 $A(B\mathbf{x})=(AB)\mathbf{x}$ から、行列積の成分表示 $$ (AB)_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj} $$ が導かれた。□
規定については以下の記事を参照して下さい。
あるいは、以下のようにベクトルの内積から自然に行列の積を定義したと考えることもできます。
証明をみる (ベクトルの内積から構築)
以下のように考えると積の定義が自然であることが分かります。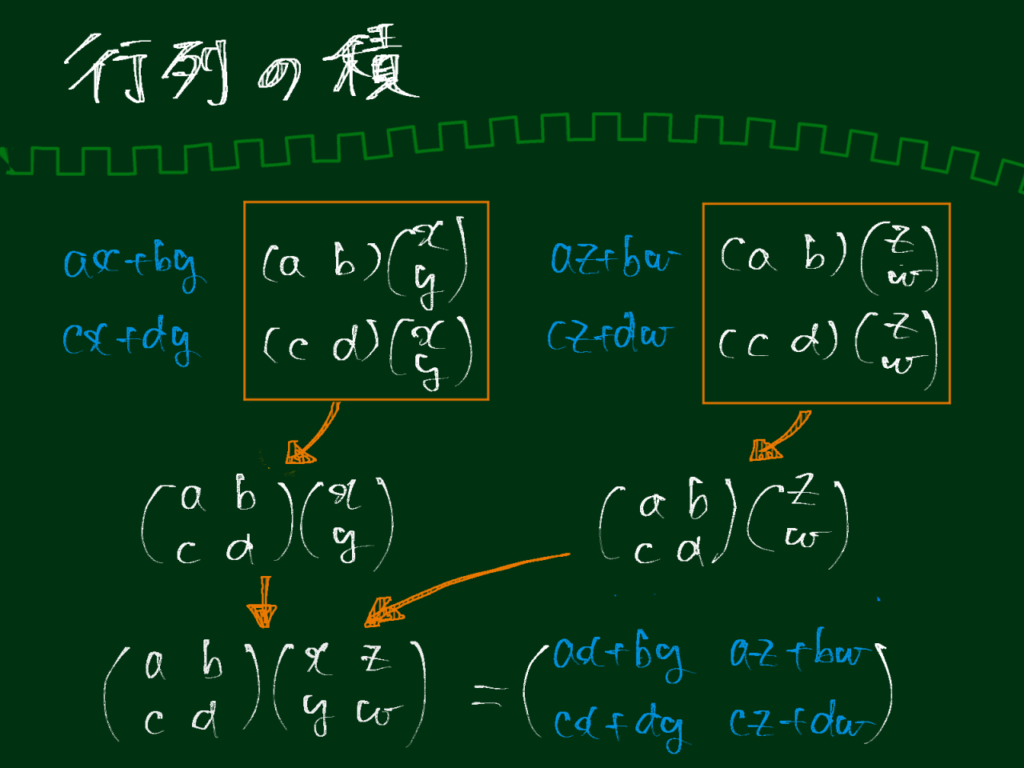
(3) 行列の積の性質(1)
結合法則
適合するサイズで $(AB)C=A(BC)$
証明をみる
成分で $$ \big((AB)C\big)_{ij}=\sum{k}(AB)_{ik}c_{kj}=\sum_k\left(\sum_{\ell}a_{i\ell}b_{\ell k}\right)c_{kj} =\sum_{\ell}a_{i\ell}\left(\sum_k b_{\ell k}c_{kj}\right) =\big(A(BC)\big)_{ij}. $$ 有限和なので和の順序交換が正当化される。よって全成分が一致する。$\square$分配法則
$A(B+C)=AB+AC$
証明をみる
成分で $$(A(B+C))_{ij}=\sum_k a_{ik}(b_{kj}+c_{kj})=\sum_k a_{ik}b_{kj}+\sum_k a_{ik}c_{kj}=(AB+AC)_{ij}.$$ 同様に $(A+B)C=AC+BC$。$\square$交換法則は不成立
一般に $AB\neq BA$
証明をみる
例えば $$ A=\begin{pmatrix}0&1\\0&0\end{pmatrix},\quad B=\begin{pmatrix}0&0\\1&0\end{pmatrix} $$ では $$ AB=\begin{pmatrix}1&0\\0&0\end{pmatrix},\quad BA=\begin{pmatrix}0&0\\0&1\end{pmatrix}, $$ と一致しません。$\square$(4) 行列の積の性質(2)：ブロックに分けて計算
行列の積は小行列（ブロック）に分割し、それに対して積の定義を適用して計算することができます。
定理3.9: 小行列を用いた行列の積
$$
A = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix},\quad
B = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix}
$$
と $2\times 2$ ブロックに分けられるとき、
$$
AB = \begin{pmatrix}
A_{11}B_{11} + A_{12}B_{21} & A_{11}B_{12} + A_{12}B_{22} \\
A_{21}B_{11} + A_{22}B_{21} & A_{21}B_{12} + A_{22}B_{22}
\end{pmatrix}
$$
となります。
イメージは以下です。
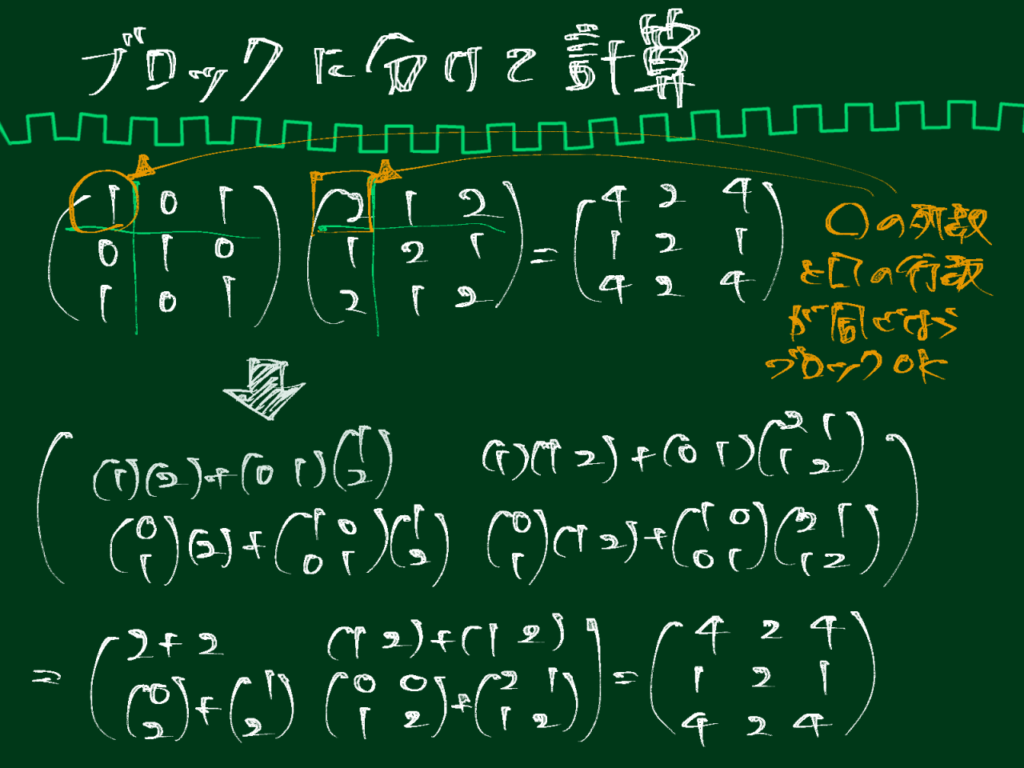
なお、ブロックによる行列の計算では、以下の点について銘記しておくと良いです。
- ブロックのサイズが噛み合っていること（掛ける内側の次元が一致）を必ず確認する。
例：$A_{12}$（$3\times2$）と $B_{21}$（$2\times2$）は掛けられるが、もし $B_{21}$ が $3\times2$ なら掛けられません。 - ゼロブロック・対角ブロック・三角ブロックがあるときは、不要な計算を省ける（効率化）。
- 理解のコツは「ブロックも行列、だからブロック同士で普通の行列積をする」。最後に同じ位置のブロックを足すだけです。
以下に実際の計算例を2つ掲載します。
具体例をみる: $4\times4$を$2\times2$のブロックにする例
$4\times4$ 行列を $2\times2$ ブロック（各ブロックは $2\times2$）に分けます。 $$ A=\begin{pmatrix} \boxed{\begin{matrix}1&2\\3&4\end{matrix}}&\boxed{\begin{matrix}5&6\\7&8\end{matrix}}\\[6pt] \boxed{\begin{matrix}0&1\\2&3\end{matrix}}&\boxed{\begin{matrix}4&0\\1&2\end{matrix}} \end{pmatrix} = \begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{pmatrix}, \quad B=\begin{pmatrix} \boxed{\begin{matrix}2&1\\0&1\end{matrix}}&\boxed{\begin{matrix}3&0\\1&2\end{matrix}}\\[6pt] \boxed{\begin{matrix}1&4\\2&0\end{matrix}}&\boxed{\begin{matrix}0&5\\2&1\end{matrix}} \end{pmatrix} = \begin{pmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{pmatrix}. $$(1) 上左ブロック $C_{11}=A_{11}B_{11}+A_{12}B_{21}$
$$ A_{11}B_{11}=\begin{pmatrix}1&2\\3&4\end{pmatrix}\begin{pmatrix}2&1\\0&1\end{pmatrix} =\begin{pmatrix} 1\cdot2+2\cdot0&1\cdot1+2\cdot1\\ 3\cdot2+4\cdot0&3\cdot1+4\cdot1 \end{pmatrix} =\begin{pmatrix}2&3\\6&7\end{pmatrix} $$ $$ A_{12}B_{21}=\begin{pmatrix}5&6\\7&8\end{pmatrix}\begin{pmatrix}1&4\\2&0\end{pmatrix} =\begin{pmatrix} 5\cdot1+6\cdot2&5\cdot4+6\cdot0\\ 7\cdot1+8\cdot2&7\cdot4+8\cdot0 \end{pmatrix} =\begin{pmatrix}17&20\\23&28\end{pmatrix} $$ $$ C_{11}=A_{11}B_{11}+A_{12}B_{21} =\begin{pmatrix}2&3\\6&7\end{pmatrix}+\begin{pmatrix}17&20\\23&28\end{pmatrix} =\begin{pmatrix}19&23\\29&35\end{pmatrix} $$
(2) 上右ブロック $C_{12}=A_{11}B_{12}+A_{12}B_{22}$
$$ A_{11}B_{12}=\begin{pmatrix}1&2\\3&4\end{pmatrix}\begin{pmatrix}3&0\\1&2\end{pmatrix} =\begin{pmatrix} 1\cdot3+2\cdot1&1\cdot0+2\cdot2\\ 3\cdot3+4\cdot1&3\cdot0+4\cdot2 \end{pmatrix} =\begin{pmatrix}5&4\\13&8\end{pmatrix} $$ $$ A_{12}B_{22}=\begin{pmatrix}5&6\\7&8\end{pmatrix}\begin{pmatrix}0&5\\2&1\end{pmatrix} =\begin{pmatrix} 5\cdot0+6\cdot2&5\cdot5+6\cdot1\\ 7\cdot0+8\cdot2&7\cdot5+8\cdot1 \end{pmatrix} =\begin{pmatrix}12&31\\16&43\end{pmatrix} $$ $$ C_{12}=\begin{pmatrix}5&4\\13&8\end{pmatrix}+\begin{pmatrix}12&31\\16&43\end{pmatrix} =\begin{pmatrix}17&35\\29&51\end{pmatrix} $$
(3) 下左ブロック $C_{21}=A_{21}B_{11}+A_{22}B_{21}$
$$ A_{21}B_{11}=\begin{pmatrix}0&1\\2&3\end{pmatrix}\begin{pmatrix}2&1\\0&1\end{pmatrix} =\begin{pmatrix} 0\cdot2+1\cdot0&0\cdot1+1\cdot1\\ 2\cdot2+3\cdot0&2\cdot1+3\cdot1 \end{pmatrix} =\begin{pmatrix}0&1\\4&5\end{pmatrix} $$ $$ A_{22}B_{21}=\begin{pmatrix}4&0\\1&2\end{pmatrix}\begin{pmatrix}1&4\\2&0\end{pmatrix} =\begin{pmatrix} 4\cdot1+0\cdot2&4\cdot4+0\cdot0\\ 1\cdot1+2\cdot2&1\cdot4+2\cdot0 \end{pmatrix} =\begin{pmatrix}4&16\\5&4\end{pmatrix} $$ $$ C_{21}=\begin{pmatrix}0&1\\4&5\end{pmatrix}+\begin{pmatrix}4&16\\5&4\end{pmatrix} =\begin{pmatrix}4&17\\9&9\end{pmatrix} $$
(4) 下右ブロック $C_{22}=A_{21}B_{12}+A_{22}B_{22}$
$$ A_{21}B_{12}=\begin{pmatrix}0&1\\2&3\end{pmatrix}\begin{pmatrix}3&0\\1&2\end{pmatrix} =\begin{pmatrix} 0\cdot3+1\cdot1&0\cdot0+1\cdot2\\ 2\cdot3+3\cdot1&2\cdot0+3\cdot2 \end{pmatrix} =\begin{pmatrix}1&2\\9&6\end{pmatrix} $$ $$ A_{22}B_{22}=\begin{pmatrix}4&0\\1&2\end{pmatrix}\begin{pmatrix}0&5\\2&1\end{pmatrix} =\begin{pmatrix} 4\cdot0+0\cdot2&4\cdot5+0\cdot1\\ 1\cdot0+2\cdot2&1\cdot5+2\cdot1 \end{pmatrix} =\begin{pmatrix}0&20\\4&7\end{pmatrix} $$ $$ C_{22}=\begin{pmatrix}1&2\\9&6\end{pmatrix}+\begin{pmatrix}0&20\\4&7\end{pmatrix} =\begin{pmatrix}1&22\\13&13\end{pmatrix} $$
(5) 組み立て（$C=AB$）
$$ C=\begin{pmatrix} \boxed{C_{11}}&\boxed{C_{12}}\\ \boxed{C_{21}}&\boxed{C_{22}} \end{pmatrix} = \begin{pmatrix} 19&23&17&35\\ 29&35&29&51\\ 4&17&1&22\\ 9&9&13&13 \end{pmatrix} $$
具体例をみる: 長方形ブロック（行列サイズが違う場合）の例
$A$ が $3\times4$、$B$ が $4\times2$とし、列方向／行方向に分割して $$ A=\bigl[A_{11}\ \ A_{12}\bigr],\quad A_{11}\in\mathbb{R}^{3\times2},\ A_{12}\in\mathbb{R}^{3\times2} $$ $$ B=\begin{bmatrix}B_{11}\\ B_{21}\end{bmatrix},\quad B_{11}\in\mathbb{R}^{2\times2},\ B_{21}\in\mathbb{R}^{2\times2} $$ このとき $$ AB=A_{11}B_{11}+A_{12}B_{21}\quad(\text{サイズ }3\times2) $$具体的に
$$ A=\begin{pmatrix} 1&2&3&4\\ 0&1&0&1\\ 2&0&1&0 \end{pmatrix}, \quad B=\begin{pmatrix} 1&0\\ 2&1\\ 0&1\\ 3&2 \end{pmatrix} $$ とし、前半2列・後半2列で分ける： $$ A_{11}=\begin{pmatrix}1&2\\0&1\\2&0\end{pmatrix},\quad A_{12}=\begin{pmatrix}3&4\\0&1\\1&0\end{pmatrix} $$ $$ B_{11}=\begin{pmatrix}1&0\\2&1\end{pmatrix},\quad B_{21}=\begin{pmatrix}0&1\\3&2\end{pmatrix} $$
(1) 各ブロックの積
$$ A_{11}B_{11}= \begin{pmatrix}1&2\\0&1\\2&0\end{pmatrix} \begin{pmatrix}1&0\\2&1\end{pmatrix} = \begin{pmatrix} 1\cdot1+2\cdot2&1\cdot0+2\cdot1\\ 0\cdot1+1\cdot2&0\cdot0+1\cdot1\\ 2\cdot1+0\cdot2&2\cdot0+0\cdot1 \end{pmatrix} = \begin{pmatrix}5&2\\2&1\\2&0\end{pmatrix} $$ $$ A_{12}B_{21}= \begin{pmatrix}3&4\\0&1\\1&0\end{pmatrix} \begin{pmatrix}0&1\\3&2\end{pmatrix} = \begin{pmatrix} 3\cdot0+4\cdot3&3\cdot1+4\cdot2\\ 0\cdot0+1\cdot3&0\cdot1+1\cdot2\\ 1\cdot0+0\cdot3&1\cdot1+0\cdot2 \end{pmatrix} = \begin{pmatrix}12&11\\3&2\\0&1\end{pmatrix} $$
(2) 和をとって $AB$
$$ AB=A_{11}B_{11}+A_{12}B_{21} =\begin{pmatrix}5&2\\2&1\\2&0\end{pmatrix} +\begin{pmatrix}12&11\\3&2\\0&1\end{pmatrix} = \begin{pmatrix}17&13\\5&3\\2&1\end{pmatrix} $$
(3) 直接計算での検算（任意）
$$ AB= \begin{pmatrix} 1&2&3&4\\ 0&1&0&1\\ 2&0&1&0 \end{pmatrix} \begin{pmatrix} 1&0\\ 2&1\\ 0&1\\ 3&2 \end{pmatrix} = \begin{pmatrix} 1\cdot1+2\cdot2+3\cdot0+4\cdot3&1\cdot0+2\cdot1+3\cdot1+4\cdot2\\ 0\cdot1+1\cdot2+0\cdot0+1\cdot3&0\cdot0+1\cdot1+0\cdot1+1\cdot2\\ 2\cdot1+0\cdot2+1\cdot0+0\cdot3&2\cdot0+0\cdot1+1\cdot1+0\cdot2 \end{pmatrix} = \begin{pmatrix}17&13\\5&3\\2&1\end{pmatrix} $$ 一致していることが確認できます。
(5) 様々な行列(4)：単位行列
定義3.10: 単位行列
対角成分がすべて $1$でそれ以外の成分が$0$ の正方行列を 単位行列 $I_n$ といいます。
単位行列はサイズが合う行列$A$について$AI=IA=A$となります。
単位行列はサイズが合う行列$A$について$AI=IA=A$となります。
(6) 様々な行列(5)：ゼロ行列
定義3.11: ゼロ行列
全成分が $0$ の行列を ゼロ行列（$O$ または $0_{m\times n}$）といいます。
(7) 様々な行列(6)：ゼロ因子
定義3.12: ゼロ因子
$A\neq O,\ B\neq O$ だが $AB=O$ となるとき，$A,B$ を零因子という。
具体例をみる
$$ A=\begin{pmatrix}1&0\\0&0\end{pmatrix},\quad B=\begin{pmatrix}0&0\\1&0\end{pmatrix}\quad\Rightarrow\quad AB=O. $$(8) 様々な行列(7)：べき零行列（ニルポテント）
定義3.13: べき零行列（ニルポテント）
ある $k\in\mathbb{N}$ で $A^k=O$となる行列をべき零行列という。
具体例をみる
$N=\begin{pmatrix}0&1\\0&0\end{pmatrix}$ は $N^2=O$。(9) 様々な行列(8)：べき等行列（イドポテント）
定義3.14: べき等行列（イドポテント）
$P^2=P$となる行列をべき等行列という。
具体例をみる
$P=\begin{pmatrix}1&0\\0&0\end{pmatrix}$ は $P^2=P$。(10) 行列の積に関する定理(1)：$a\mathbf{x}+b\mathbf{y}+c\mathbf{z}$の分解
定理3.15: 積への分解①
$$
a\mathbf{x}+b\mathbf{y}+c\mathbf{z}=(\mathbf{x}\ \mathbf{y}\ \mathbf{z})\begin{pmatrix}a\\b\\c\end{pmatrix}.
$$
(11) 行列の積に関する定理(2)：$(a\mathbf{x},\,b\mathbf{y},\,c\mathbf{z})$の分解
定理3.16: 積への分解②
$$
(a\mathbf{x}\ \ b\mathbf{y}\ \ c\mathbf{z})=(\mathbf{x}\ \mathbf{y}\ \ \mathbf{z})\,\mathrm{diag}(a,b,c).
$$
(12) 行列の積に関する定理(3)： $(a\mathbf{x},\,\mathbf{x}+b\mathbf{y},\,\mathbf{y}+c\mathbf{z})$の分解
定理3.16: 積への分解③
$$
(a\mathbf{x}\ \ \mathbf{x}+b\mathbf{y}\ \ \mathbf{y}+c\mathbf{z})
=(\mathbf{x}\ \mathbf{y}\ \mathbf{z})
\begin{pmatrix}
a&1&0\\
0&b&1\\
0&0&c
\end{pmatrix}.
$$
(13) 行列の積に関する定理(4)：対角行列の積
定理3.17: 対角行列の積
$$
\operatorname{diag}(a_1,\dots,a_n)\cdot \operatorname{diag}(b_1,\dots,b_n)
=\operatorname{diag}(a_1b_1,\dots,a_nb_n).
$$
証明をみる
積の $(i,j)$ 成分は $\sum_k a_i\delta_{ik}\,b_k\delta_{kj}=a_i b_i\delta_{ij}$。$\square$(14) 行列の積に関する定理(5)：三角行列の積
定理3.18: 三角行列の積
上三角行列 $U,V$ に対し $UV$ も上三角行列で対角は $(u_{ii}v_{ii})$。
証明をみる
$n\times n$ 行列 $U=(u_{ij})$，$V=(v_{ij})$ が**上三角**であるとは $$ u_{ij}=0\ (i>j),\qquad v_{ij}=0\ (i>j) $$ すなわち，主対角線より下の成分がすべて $0$ であることをいう。このとき，積 $W=UV=(w_{ij})$ は上三角で，さらに $$ w_{ii}=u_{ii}\,v_{ii}\quad(1\le i\le n) $$ が成り立つことを示す。
証明（添字の条件を丁寧に追う）
積の成分は定義より $$ w_{ij}=(UV)_{ij}=\sum_{k=1}^{n}u_{ik}v_{kj}. $$
1) $W$ が上三角であること（$i>j$ のとき $w_{ij}=0$）
上三角の条件を「非ゼロになりうる $k$ の範囲」として書き直すと
– $u_{ik}\ne0$ になりうるのは **$i\le k$**（行より列が右側）
– $v_{kj}\ne0$ になりうるのは **$k\le j$**（行が列の上）
よって $u_{ik}v_{kj}$ が**両方**非ゼロになりうるには $$ i\le k\le j $$ が必要。ところが今 $i>j$（主対角線より下）を仮定しているので，この不等式を満たす $k$ は**存在しない**。したがって和の各項がすべて $0$ になり $$ w_{ij}=0\qquad(i>j). $$ ゆえに $W$ は上三角。
2) 対角成分（$i=j$）の式 $w_{ii}=u_{ii}v_{ii}$
同様に $$ w_{ii}=\sum_{k=1}^{n}u_{ik}v_{ki}. $$ ここで非ゼロになりうる条件を併せると
– $u_{ik}\ne0$ のためには **$i\le k$**
– $v_{ki}\ne0$ のためには **$k\le i$**
両方を同時に満たすには $$ i\le k\le i\ \Rightarrow\ k=i $$ しかない。したがって和には $k=i$ の項だけが残り $$ w_{ii}=u_{ii}\,v_{ii}. $$
以上で主張が示された。□
具体例をみる
$$ U=\begin{pmatrix}u_{11}&u_{12}&u_{13}\\0&u_{22}&u_{23}\\0&0&u_{33}\end{pmatrix},\ V=\begin{pmatrix}v_{11}&v_{12}&v_{13}\\0&v_{22}&v_{23}\\0&0&v_{33}\end{pmatrix}. $$ このとき $$ UV=\begin{pmatrix} u_{11}v_{11}&u_{11}v_{12}+u_{12}v_{22}&u_{11}v_{13}+u_{12}v_{23}+u_{13}v_{33}\\ 0&u_{22}v_{22}&u_{22}v_{23}+u_{23}v_{33}\\ 0&0&u_{33}v_{33} \end{pmatrix}, $$ 確かに下三角はゼロ，対角は $(u_{11}v_{11},u_{22}v_{22},u_{33}v_{33})$ になっている。(13) まとめ
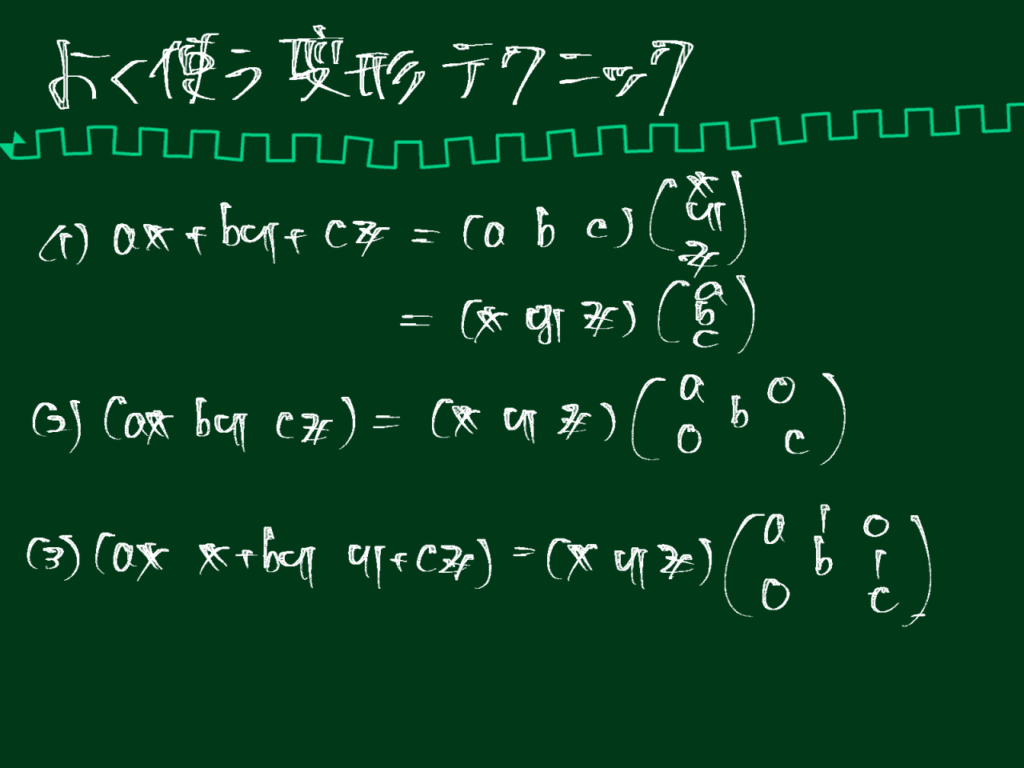
5. 行列式
複数の方程式をまとめた行列による方程式について、各々の方程式を解かずに行列のまま解くことができれば計算が楽になります。
そのためには$AA^{-1}=A^{-1}A=I$となる逆行列$A^{-1}$という概念を導入します。
これで$AX=B$のような方程式については両辺に左から$A^{-1}$をかけて$X=A^{-1}B$として解くことができます。
逆行列は行列式という概念を用いて定義されるため、本節では行列式について説明をします。
ただし本節では2次または3次の正方行列の行列式を具体的に紹介するにとどめ、n次正方行列に対する詳しい行列式の定義や説明は以下の記事に譲ります。
(1) 行列式の定義
以下の定義の意味は上記で紹介した「行列式」の記事で詳細を説明しています。本節では参考程度に載せており、現段階では無理に理解する必要はありません。
定義3.19: 行列式の定義
$n\times n$ 行列 $A=(a_{ij})$ の行列式$\det A$または$|A|$は
$$
\det(A)=\sum_{\sigma\in S_n}\operatorname{sgn}(\sigma)\prod_{i=1}^n a_{i,\sigma(i)}.
$$
ここで $S_n$ は $n$ 元対称群，$\operatorname{sgn}(\sigma)\in{+1,-1}$ は置換の符号。
(2) 行列式に関する公式(1)：2次正方行列の行列式
定理3.20: 2次正方行列の行列式の公式
2次正方行列の行列式の公式は以下。
$$
\det\begin{pmatrix}a&b\\ c&d\end{pmatrix}
=ad-bc.
$$
証明をみる
2次正方行列の公式は以下のように導出できる。 $$ \det\begin{pmatrix}a&b\\ c&d\end{pmatrix} =\operatorname{sgn}(\mathrm{id})\,a d+\operatorname{sgn}((12))\,b c=ad-bc. $$ （$S_2={\mathrm{id},(12)}$，後者は奇置換で符号 $-$。）$\square$具体例をみる
次の 2 次正方行列を考えます。 $$ A=\begin{pmatrix} 3&-2\\ 5&4 \end{pmatrix} $$ 2×2 行列の行列式の公式は $$ \det\begin{pmatrix} a&b\\ c&d \end{pmatrix}=ad-bc $$ です。これを $A$ に適用すると，$a=3,\ b=-2,\ c=5,\ d=4$ なので1. 斜めの積を計算： $$ ad=3\cdot4=12,\qquad bc=(-2)\cdot5=-10 $$
2. 差をとる（$ad-bc$）： $$ \det A=12-(-10)=12+10=22 $$
**結論**： $$ \boxed{\det A=22} $$
(3) 行列式に関する公式(2)：3次正方行列の行列式
定理3.21: 3次正方行列の行列式の公式(サラスの公式)
3次正方行列の行列式は以下で与えられます。
$$
\det\begin{pmatrix}a&b&c\\ d&e&f\\ g&h&i\end{pmatrix}
=aei+bfg+cdh-ceg-bdi-afh.
$$
以下にイメージも載せておきます。
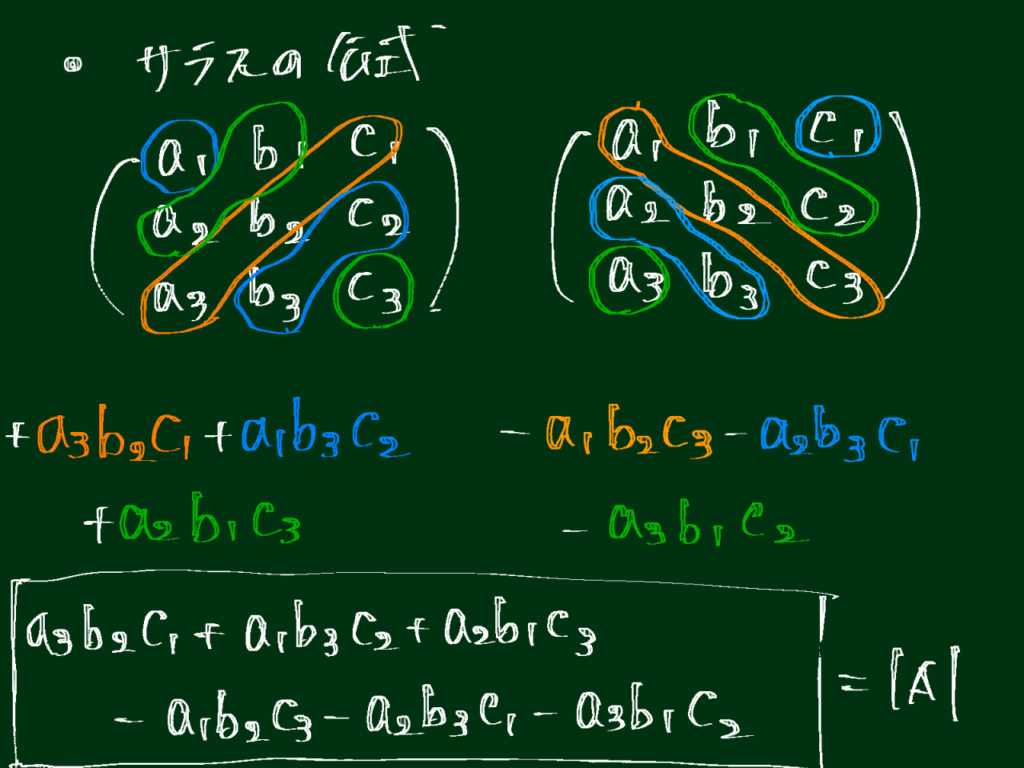
証明をみる
1行目で余因子展開（ラプラス展開）すると $$ \det A =a\begin{vmatrix}e&f\\h&i\end{vmatrix} -b\begin{vmatrix}d&f\\g&i\end{vmatrix} +c\begin{vmatrix}d&e\\g&h\end{vmatrix}. $$ 各 $2\times2$ 行列式を計算すると $$ \begin{vmatrix}e&f\\h&i\end{vmatrix}=ei-fh,\qquad \begin{vmatrix}d&f\\g&i\end{vmatrix}=di-fg,\qquad \begin{vmatrix}d&e\\g&h\end{vmatrix}=dh-eg. $$ したがって $$ \det A =a(ei-fh)-b(di-fg)+c(dh-eg). $$ 右辺を展開・整理すると $$ \det A =aei-afh-bdi+bfg+cdh-ceg. $$ 並べ替えると $$ \det A =\underbrace{aei+bfg+cdh}_{\text{正の和}} -\underbrace{(ceg+bdi+afh)}_{\text{負の和}}. $$ これがサラスの公式そのものである。□余因子展開については以下の記事を参照して下さい。
具体例をみる
次の 3 次正方行列を考えます。 $$ A=\begin{pmatrix} 2 & 3 & 1 \\ 4 & 1 & -2 \\ -1 & 5 & 3 \end{pmatrix} $$1. **最初の 2 列を右に書き足す**
$$ \begin{array}{ccc|cc} 2 & 3 & 1 & 2 & 3 \\ 4 & 1 & -2 & 4 & 1 \\ -1 & 5 & 3 & -1 & 5 \end{array} $$
2. **左上から右下への3本の対角線の積の和を求める**
– 1本目：$2 \times 1 \times 3 = 6$
– 2本目：$3 \times (-2) \times (-1) = 6$
– 3本目：$1 \times 4 \times 5 = 20$
和： $$ 6 + 6 + 20 = 32 $$
3. **右上から左下への3本の対角線の積の和を求める**
– 1本目：$1 \times 1 \times (-1) = -1$
– 2本目：$2 \times (-2) \times 5 = -20$
– 3本目：$3 \times 4 \times 3 = 36$
和： $$ -1 + (-20) + 36 = 15 $$
4. **差をとる（右下方向の和 − 左下方向の和）** $$ \det A = 32 – 15 = 17 $$
**結論**： $$ \boxed{\det A = 17} $$
6. 逆行列
逆行列は行列で表現した方程式をそのまま解く際などに用います。これにより、行列としてまとめる前の個々の方程式を個別に解かずに一括して解くことができるようになります。
(1) 様々な行列(9)：逆行列の定義
定義3.22: 逆行列
正方行列 $A$の逆行列は$AB=BA=I$を満たす$B$のことで$B=A^{-1}$と表記する。
(2) 正則の定義
定義3.23: 正則
正方行列 $A$ が 正則 とは，$A^{-1}$ が存在し $AA^{-1}=A^{-1}A=I$ を満たすこと。
(3) 余因子の定義
余因子は一般の行列式の計算や逆行列の計算に用いる概念であり「行列式」の記事で詳しく解説しています。定義の背景などはそちらの記事を参考にし、本節では定義のみ掲載しておきます。
定義3.24: 余因子
$C_{ij}=(-1)^{i+j}M_{ij}$（$M_{ij}$ は $i$ 行 $j$ 列を除いた小行列の行列式）を余因子という。
(4) 様々な行列(10)：余因子行列の定義
余因子行列は逆行列の定義や計算に用いる概念であり「行列式」の記事で詳しく解説しています。定義の背景などはそちらの記事を参考にし、本節では定義のみ掲載しておきます。
定義3.25: 余因子行列
余因子 $C_{ij}=(-1)^{i+j}M_{ij}$ を並べた行列 $C=(C_{ij})$ の転置
$$\operatorname{adj}(A)=C^T$$
を 余因子行列 という。
(5) 余因子行列に関する定理(1)：基本恒等式
余因子行列の基本恒等式は余因子行列によって逆行列を表すために用いる定理です。「行列式」の記事で詳しく解説しています。定義の背景などはそちらを参考にし、本節では定義のみ掲載しておきます。
定理3.26: 余因子行列の基本恒等式
余因子行列について、以下の基本恒等式が成立する。
$A\,\operatorname{adj}(A)=\operatorname{adj}(A)\,A=\det(A)\,I$
証明をみる
$(A\,\operatorname{adj}(A)){ij}=\sum{k=1}^n a_{ik}C_{jk}$ である。 $i=j$ のとき：$\displaystyle \sum_k a_{ik}C_{ik}$ は $i$ 行に沿う余因子展開そのもので $\det(A)$。 $i\neq j$ のとき：$A$ の 第 $i$ 行を第 $j$ 行に置き換えた行列 を $A’$ とすると 2 行が等しく $\det(A’)=0$。一方，$\det(A’)$ を第 $j$ 行に沿って展開すると $$ \det(A’)=\sum_k a_{ik}C_{jk}=(A\,\operatorname{adj}(A))_{ij}. $$ よって $(A\,\operatorname{adj}(A)){ij}=0$。 以上から $$ A\,\operatorname{adj}(A)=\det(A)\,I. $$ 右側乗でも同様に示せる。$\square$(6) 逆行列に関する定理(1)：逆行列の表現
余因子行列を利用して逆行列を求めることができます。詳しくは「行列式」の記事で詳しく解説しています。詳しい証明などはそちらを参考にし、本節では結論と簡単な証明のみ掲載しておきます。
定理3.27: 逆行列の余因子行列による表現
基本恒等式を用いると、以下のように逆行列を与えることができる。
$\det(A)\neq 0$ なら
$$
\boxed{\ A^{-1}=\frac{1}{\det(A)}\,\operatorname{adj}(A)\ }.
$$
(7) 逆行列に関する公式(2)：2次正方行列の逆行列の公式
定理3.28: 2次正方行列の逆行列の公式
2次正方行列の逆行列は以下。
$$A^{-1}=\frac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}.$$
証明をみる
$A$ の $(i,j)$ 成分の**余因子** $C_{ij}$ を $$ C_{ij}=(-1)^{i+j}M_{ij}, $$ ここで $M_{ij}$ は $A$ の第 $i$ 行第 $j$ 列を除いた小行列（$2\times2$ の場合は $1\times1$）の行列式とする。 $2\times2$ のときは $$ M_{11}=d,\quad M_{12}=c,\quad M_{21}=b,\quad M_{22}=a, $$ したがって $$ C_{11}=d,\quad C_{12}=-c,\quad C_{21}=-b,\quad C_{22}=a. $$ **余因子行列**（cofactor matrix）は $$ C=\begin{pmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{pmatrix} =\begin{pmatrix}d&-c\\-b&a\end{pmatrix}, $$ **随伴行列**（adjugate，adjoint）はその転置 $$ \operatorname{adj}(A)=C^{\mathsf T} =\begin{pmatrix}d&-b\\-c&a\end{pmatrix}. $$次に、以下の恒等式を2×2 で直接計算して確かめる。 $$ A\,\operatorname{adj}(A)=\det(A)\,I. $$ 左辺を成分計算すると $$ A\,\operatorname{adj}(A) =\begin{pmatrix}a&b\\c&d\end{pmatrix} \begin{pmatrix}d&-b\\-c&a\end{pmatrix} =\begin{pmatrix} ad-bc&-ab+ab\\ cd-dc&-bc+ad \end{pmatrix} =\begin{pmatrix} ad-bc&0\\ 0&ad-bc \end{pmatrix} =(ad-bc)I. $$ 右辺は $\det(A)\,I=(ad-bc)I$ なので一致する。
従って、$\det(A)\neq0$ ならば，上の恒等式の両辺を $\det(A)$ で割って $$ A\left(\frac{1}{\det(A)}\operatorname{adj}(A)\right)=I $$ が得られる。よって $$ A^{-1}=\frac{1}{\det(A)}\operatorname{adj}(A). $$
2×2 では具体的に $$ \det(A)=ad-bc,\qquad \operatorname{adj}(A)=\begin{pmatrix}d&-b\\-c&a\end{pmatrix} $$ だから $$ \boxed{\; A^{-1}=\frac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}\; } $$
(8) 逆行列に関する公式(3)：対角行列の逆行列
定理3.29:対角行列の逆行列
$$
D=\operatorname{diag}(d_1,\dots,d_n),\ d_i\ne0\ \Rightarrow\
D^{-1}=\operatorname{diag}\Big(\frac1{d_1},\dots,\frac1{d_n}\Big).
$$
証明をみる
$DD^{-1}=\operatorname{diag}(d_1\cdot \tfrac1{d_1},\dots)=I$。逆も同様。$\square$7. 転置
(1) 様々な行列(11)：転置行列の定義
定義3.30: 転置と転置行列
$A=(a_{ij})$ の 転置 は $A^T=(a_{ji})$。行と列を入れ替える操作。
また、$A^T$を$A$の転置行列という。
また、$A^T$を$A$の転置行列という。
(2) 様々な行列(12)：随伴行列の定義
定義3.31: 随伴行列
複素数体上では随伴（共役転置） を $A^*=\overline{A}^T$ と定める（実行列なら $A^*=A^T$）。
また、$A^*$を$A$の随伴行列という。
また、$A^*$を$A$の随伴行列という。
(3) 転置に関する定理(1)：積の転置
定理3.32: 積の転置
$(AB)^T=B^TA^T$
証明をみる
成分で $$ (AB)^T_{ij}=(AB)_{ji}=\sum_k a{jk}b_{ki}=\sum_k b_{ki}a_{jk}=(B^TA^T)_{ij}. \square $$(4) 転置に関する定理(2)：逆行列の転置
定理3.33: 逆行列の転置
$(A^{-1})^T=(A^T)^{-1}$
証明をみる
$AA^{-1}=I$ を転置して $(A^{-1})^TA^T=I$。$\square$(5) 転置に関する定理(3)：転置行列の行列式
定理3.34: 転置行列の行列式
$\det(A^T)=\det(A)$
証明をみる
置換定義は行版・列版で同値，あるいは余因子展開を行方向・列方向いずれでしても値は同じ。$\square$置換や余因子展開については以下の記事を参照。
8. トレース
(1) トレースの定義
定義3.35: トレースの定義
正方行列 $A=(a_{ij})$ の トレース は主対角の和：
$$\operatorname{tr}(A)=\sum_{i=1}^n a_{ii}.$$
(2) トレースに関する定理(1)：積のトレースの循環性
定理3.36: 積のトレースの循環性
トレースについて以下の2式が成立する。
$$\operatorname{tr}(AB)=\operatorname{tr}(BA)$$
$$\operatorname{tr}(ABC)=\operatorname{tr}(BCA)=\operatorname{tr}(CAB)$$
証明をみる
$$ \operatorname{tr}(AB)=\sum_{i}(AB)_{ii} =\sum_i\sum_j a_{ij}b_{ji} =\sum_j\sum_i b_{ji}a_{ij} =\sum_j(BA)_{jj} =\operatorname{tr}(BA). $$ 有限和なので順序交換が正当化される。さらに同様の帰納で $\operatorname{tr}(ABC)=\operatorname{tr}(BCA)=\operatorname{tr}(CAB)$ も成り立つ。$\square$(3) トレースに関する定理(2)：自身の転置との積（フロベニウスノルム）
定理3.37: フロベニウスノルム
$\langle A,B\rangle_F=\operatorname{tr}(A^TB)$をフロベニウス内積といい、以下が成立する。
$$
\langle A,A\rangle_F = \operatorname{tr}(A^TA)=\sum_{i,j} a_{ij}^2
$$
フロベニウスノルムについては以下の記事も参照して下さい。
証明をみる
$$ \operatorname{tr}(A^TA)=\sum_i (A^TA)_{ii} =\sum_i\sum_j a_{ji}a_{ji} =\sum_{i,j} a_{ij}^2. $$ 右辺はフロベニウスノルム $|A|_F^2$。$\square$(4) トレースに関する定理(3)：2次形式のトレース
定理3.38: 2次形式のトレース
列ベクトル $\mathbf{x}\in\mathbb{R}^n$ に対して
$$\mathbf{x}^TA\mathbf{x}=\operatorname{tr}\big(A\,\mathbf{x}\mathbf{x}^T\big)$$
2次形式については以下の記事も参照して下さい。
コメント