1. スペクトル分解とn乗
(1) スペクトル分解
定理12.1: スペクトル分解
$A\in\mathbb{C}^{n\times n}$ が（正規でなくても）対角化可能で、固有値の取り得る値が相異なるものとして ${\lambda_1,\dots,\lambda_k}$（代数重複度をまとめた「異なる値」の集合）であるとする。このとき
$$ A=\sum_{i=1}^k \lambda_i P_i,\qquad A^n=\sum_{i=1}^k \lambda_i^{\,n}P_i\ (n\in\mathbb{N}) $$と表せる。ただし $P_i$ は $V(\lambda_i)$（固有空間）への射影行列で、一般には直交射影ではない（$P_i^\ast\ne P_i$ でもよい）。特に $P_i$ は$\ell_i(t)$を定義11.17の基底多項式とすると、
$$ P_i=\ell_i(A)=\prod_{j\ne i}\frac{A-\lambda_j I}{\lambda_i-\lambda_j} $$で与えられる。
証明をみる
多項式 $q(t) = \sum_i \lambda_i \ell_i(t)$ は恒等的に $t$ に等しい。これは$A$の固有値の数を$r$個とすると、$q(t)$が$(r-1)$次式にもかかわらず、$r$個の固有値$\lambda_i\,(i=1, \cdots, r)$について$q(\lambda_i)=\lambda_i$となることから、$q(t)=t$以外考えられないためである。従って、 $$ A=\Big(\sum_{i=1}^k \lambda_i \ell_i\Big)(A)=\sum_{i=1}^k \lambda_i P_i. $$ また、定理11.20と定理11.21より、$P_iP_j=O$で$\sum_{i=1}^{n}P_i=E$であるから、$A^n = (\sum_{i=1}^k \lambda_i P_i)^n = \lambda_i^n P_i$となる。
(2) 正規行列のスペクトル分解
定理12.2: 正規行列のスペクトル分解
$A$ が正規行列（$AA^\ast=A^\ast A$）なら、固有空間 $V(\lambda_i)$ 同士は直交し、$A$ は
$$
A=\sum_{i=1}^k \lambda_i P_i,\qquad A^n=\sum_{i=1}^k \lambda_i^{\,n}P_i
$$
と表せる。
ここで$P_i$は、$A$の固有ベクトル$\mathbf{u}_i\,(i=1, \cdots, n)$を用いて以下。
$$ P_i = \mathbf{u_i}\mathbf{u_i}^T $$ ※ 正規行列については以下の記事を参照して下さい。
ここで$P_i$は、$A$の固有ベクトル$\mathbf{u}_i\,(i=1, \cdots, n)$を用いて以下。
$$ P_i = \mathbf{u_i}\mathbf{u_i}^T $$ ※ 正規行列については以下の記事を参照して下さい。
証明をみる
定理12.1のスペクトル分解より $$ A=\sum_{i=1}^k \lambda_i P_i,\qquad A^n=\sum_{i=1}^k \lambda_i^{\,n}P_i $$ は自明なので、以下を示す。 $$ P_i = \mathbf{u_i}\mathbf{u_i}^T $$$A$は正規行列だから、$A$の固有ベクトル$\mathbf{u}_i\,(i=1, \cdots, n)$を並べた行列$Q$を用いて$A=QDQ^\ast$と分解できる。ここで$D$は$A$の固有値を対角成分に並べた対角行列。
従って、$P_i = \ell_i(A) = \ell_i(QDQ^\ast) = Q\ell_i(D)Q^\ast$。なお、この変形は定理11.19の射影作用素の公式の導出過程と同様にして示せる。
ここで、$\ell_i(D)$は$i$行目のみ$1$で他が$0$である対角行列だから$\ell_i(D)Q^\ast = (\mathbf{0}, \cdots, \mathbf{u}_i, \cdots, \mathbf{0})^T$。従って、
$$ \begin{align} P_i &= (\mathbf{u}_1, \cdots, \mathbf{u}_n)(\mathbf{0}, \cdots, \mathbf{u}_i, \cdots, \mathbf{0})^T \\ &= \mathbf{u}_i \mathbf{u}_i^T \end{align} $$ となる。2. 特異値分解
(1) 特異値分解
定理12.3: 特異値分解
任意の $A\in\mathbb{C}^{m\times n}$ について、$r = \mathrm{rank}A$とすると、$AA^\ast \in \mathbb{R}^{m \times m}$の固有ベクトルを並べたユニタリ行列 $U\in\mathbb{C}^{m\times r}$と$A^\ast A \in \mathbb{R}^{n \times n}$の固有ベクトルを並べたユニタリ行列$V\in\mathbb{C}^{n\times r}$は同じ固有値$\lambda_i\, (i=1, \cdots, r)$をもち、$\sqrt{\lambda_i} = \sigma_i$を対角成分とした対角行列 $\Sigma\in\mathbb{R}^{r\times r}$ を用いて
$$
A=U\Sigma V^\ast
$$
と書ける。
なお、$\sigma_i$については以下が成立する。 $$ A\mathbf{v}_i = \sigma_i\mathbf{u}_i \\ A\mathbf{u}_i = \sigma_i\mathbf{v}_i $$
このとき、$\Sigma$ の非零対角 $\sigma_1\ge\cdots\ge\sigma_r>0$ を 特異値といい、$U$ の対応列 $\mathbf{u}_i$ を 左特異ベクトル、$V$ の対応列 $\mathbf{v}_i$ を 右特異ベクトル という。
なお、$\sigma_i$については以下が成立する。 $$ A\mathbf{v}_i = \sigma_i\mathbf{u}_i \\ A\mathbf{u}_i = \sigma_i\mathbf{v}_i $$
このとき、$\Sigma$ の非零対角 $\sigma_1\ge\cdots\ge\sigma_r>0$ を 特異値といい、$U$ の対応列 $\mathbf{u}_i$ を 左特異ベクトル、$V$ の対応列 $\mathbf{v}_i$ を 右特異ベクトル という。
特異値分解のイメージは以下。
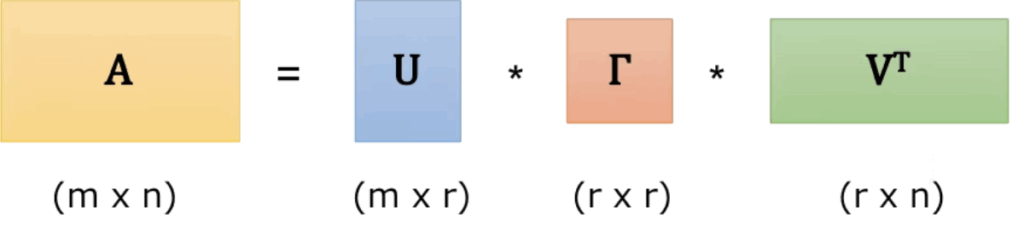
以下のように記載することもあるので、注意。
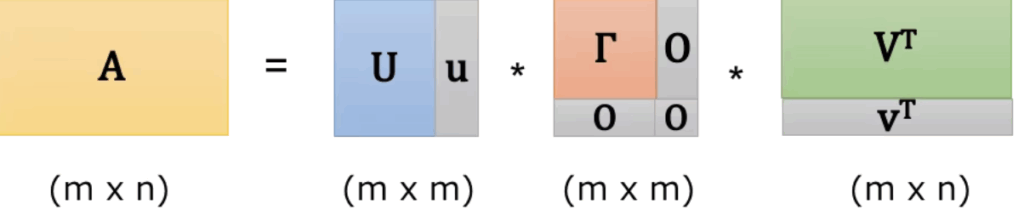
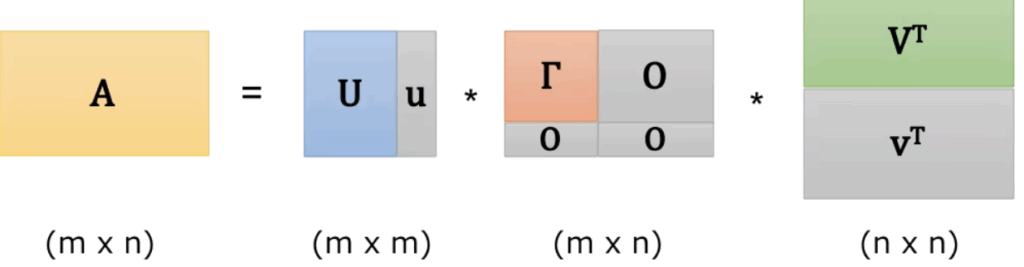
証明をみる
$AA^\ast \mathbf{u_i}=\lambda_{u_i}\mathbf{u_i}$かつ$A^\ast A\mathbf{v_i}=\lambda_{v_i}\mathbf{v_i}$となる。
従って、 $$ A^\ast A (A^\ast \mathbf{u_i}) = \lambda_{u_i}(A^{\ast}\mathbf{u_i}) $$ を$A^\ast A\mathbf{v_i}=\lambda_{v_i}\mathbf{v_i}$と比べることで、$\lambda_{u_i} = \lambda_{v_i}$でかつ$A^{\ast}\mathbf{u_i} = \sigma_{u_i}\mathbf{v_i}$となることが分かる。ここで$\sigma_{u_i}$は$\mathbf{v_i}$を規格化するための係数。また、 $$ AA^\ast (A \mathbf{v_i}) = \lambda_{v_i}(A\mathbf{v_i}) $$ を$AA^\ast \mathbf{u_i}=\lambda_{u_i}\mathbf{u_i}$と比べることで、$\lambda_{v_i} = \lambda_{u_i}$でかつ$A\mathbf{v_i} = \sigma_{v_i}\mathbf{u_i}$となることが分かる。ここで$\sigma_{v_i}$は$\mathbf{u_i}$を規格化するための係数。
従って、 $$ AA^\ast \mathbf{u_i} = \sigma_{u_i}A\mathbf{v_i} = \sigma_{u_i}\sigma_{v_i}\mathbf{u_i} $$ かつ $$ A^\ast A\mathbf{v_i} = \sigma_{v_i}A^\ast\mathbf{u_i} = \sigma_{v_i}\sigma_{u_i}\mathbf{v_i} $$ よって、$\lambda_{u_i}=\lambda_{v_i}$を$\lambda_i$とおけば$\lambda_i=\sigma_{v_i}\sigma_{u_i}$。
一方、$A^\ast\mathbf{u_i}=\sigma_{u_i}\mathbf{v_i}$を$i$について横に並べると$A^\ast U = V \mathrm{diag}(\sigma_{u_1}, \cdots, \sigma_{u_r})$。従って、$A^\ast = V \mathrm{diag}(\sigma_{u_1}, \cdots, \sigma_{u_r}) U^\ast$。
同様に、$A\mathbf{v_i}=\sigma_{v_i}\mathbf{u_i}$を$i$について横に並べると$AV = U \mathrm{diag}(\sigma_{v_1}, \cdots, \sigma_{v_r})$。従って、$A = U \mathrm{diag}(\sigma_{v_1}, \cdots, \sigma_{v_r}) V^\ast$。
上記2式を比べると、 $$ \begin{align} A &= U \mathrm{diag}(\sigma_{v_1}, \cdots, \sigma_{v_r}) V^\ast \\ &= (A^\ast)^\ast \\ &= (V \mathrm{diag}(\sigma_{u_1}, \cdots, \sigma_{u_r}) U^\ast)^\ast \\ &= U \mathrm{diag}(\sigma_{u_1}, \cdots, \sigma_{u_r}) V^\ast \end{align} $$ となるから、真ん中の対角行列は等しく、$\sigma_{u_i} = \sigma_{v_i}$。従って、$\sigma_{u_i} = \sigma_{v_i} = \sigma_i$とおき、これを$\lambda_i=\sigma_{v_i}\sigma_{u_i}$に代入すると、$\sqrt{\lambda_i} = \sigma_i$。
以上より、 $$ A = U \mathrm{diag}(\sigma_1, \cdots, \sigma_r) V^\ast = U \Sigma V^\ast $$ また、$A^\ast\mathbf{u_i}=\sigma_{u_i}\mathbf{v_i}$から$A^\ast\mathbf{u_i} = \sigma_i\mathbf{v_i}$、$A\mathbf{v_i}=\sigma_{v_i}\mathbf{u_i}$から$A\mathbf{v_i}=\sigma_i\mathbf{u_i}$も明らか。
具体例をみる
$A=\begin{pmatrix}3&1\\0&2\end{pmatrix}$を特異値分解する。1) $A^\ast A$ の固有値：実行列なので $A^\ast=A^{\mathsf T}$。 $$ A^\ast A=\begin{pmatrix}3&0\\1&2\end{pmatrix}\begin{pmatrix}3&1\\0&2\end{pmatrix}=\begin{pmatrix}9&3\\3&5\end{pmatrix} $$ 特性方程式 $$ \det\big(A^\ast A-\lambda I\big)=\begin{vmatrix}9-\lambda&3\\3&5-\lambda\end{vmatrix}=(9-\lambda)(5-\lambda)-9=\lambda^2-14\lambda+36. $$ よって $$ \lambda_{1,2}=7\pm\sqrt{13}. $$
2) 特異値： $$ \sigma_1=\sqrt{7+\sqrt{13}},\qquad \sigma_2=\sqrt{7-\sqrt{13}}. $$
3) 右特異ベクトル：$\big(A^\ast A-\lambda I\big)\mathbf{v}=\mathbf{0}$ より、$(9-\lambda)x+3y=0$ を用いて $$ \mathbf{v}_1\propto\begin{pmatrix}3\\ \lambda_1-9\end{pmatrix} =\begin{pmatrix}3\\ -2+\sqrt{13}\end{pmatrix},\qquad \mathbf{v}_2\propto\begin{pmatrix}3\\ \lambda_2-9\end{pmatrix} =\begin{pmatrix}3\\ -2-\sqrt{13}\end{pmatrix}. $$ 正規化して $V=[\widehat{\mathbf{v}}_1\ \widehat{\mathbf{v}}_2]$ を作る（$|\mathbf{v}_i|$ を各自計算して割る）。
4) 左特異ベクトル：$\mathbf{u}_i=\dfrac{1}{\sigma_i}A\,\widehat{\mathbf{v}}_i$ で得る（これも正規化されている）。$U=[\mathbf{u}_1\ \mathbf{u}_2]$。
5) 確認：$\Sigma=\mathrm{diag}(\sigma_1,\sigma_2)$ として $A=U\Sigma V^\ast$ を数値代入で確認できる。
(2) 特異値分解に関する定理(1)：特異値の数とランク
定理12.4: 特異値の数とランク
$A$ の非零特異値の本数は $\mathrm{rank}(A)$ に等しい。
証明をみる (ユニタリ変換の性質を利用)
$A=U\Sigma V^\ast$ とし、$\Sigma$ の非零対角の個数が $r$ とする。ユニタリ（直交）変換は階数を変えないので $$ \mathrm{rank}(A)=\mathrm{rank}(\Sigma)=r, $$ 一方で $r$ は非零特異値の数。証明をみる (半正定値行列の性質を利用)
$A^\ast A$ の固有値は $\sigma_i^2$（特異値の二乗）で、$\mathrm{rank}(A^\ast A)=\mathrm{rank}(A)$。半正定値行列の階数は正の固有値の個数に等しいから、非零特異値の個数と一致する。$\square$(3) 特異値分解に関する定理(2)：フロベニウスノルム
定理12.5: フロベニウスノルム
$\sigma_i\,(i=1, \cdots)$を$A$の特異値とすると、
$$
|A|_F^2:=\sum_{i,j}|a_{ij}|^2=\sum_{i=1}^{\min(m,n)}\sigma_i^2.
$$
が成り立つ。
証明をみる
定理3.37の全成分の2乗和とトレースの関係と特異値分解より $$ |A|_F^2=\mathrm{tr}(A^\ast A)=\mathrm{tr}(V\Sigma^\ast U^\ast U\Sigma V^\ast)=\mathrm{tr}(V\Sigma^2 V^\ast) $$ となる。ここで定理3.36より、$\mathrm{tr}(AB)=\mathrm{tr}(BA)$で、$A=V\Sigma^2$、$B=V^\ast$とすれば$\mathrm{tr}(V\Sigma^2 V^\ast)=\mathrm{tr}(V^\ast V\Sigma^2)=\mathrm{tr}(\Sigma^2)=\sum_i \sigma_i^2$$\square$
(4) 特異値分解に関する定理(3)：スペクトル分解の一般化
定理12.6: スペクトル分解の一般化
$r=\mathrm{rank}(A)$、$\mathbf{u}_i$を$A$の左特異ベクトル、$\mathbf{v_i}$を$A$の右特異ベクトルとすると、
$$
A=\sum_{i=1}^r \sigma_i\,\mathbf{u}_i\mathbf{v}_i^\ast
$$
と分解できる。
コメント