1. 行列の定義
(1) 行列の定義
定義3.1: 行列
行列はベクトルを並べたものです。$m$ 行 $n$ 列の行列は $m$ 本の行ベクトル（または $n$ 本の列ベクトル）を長方形に並べたもので，
$$
A = (a_{ij})=
\begin{pmatrix}
a_{11} & a_{12} & \dots & a_{1n} \\
a_{21} & a_{22} & \dots & a_{2n} \\
\vdots & \vdots & \ddots & \vdots \\
a_{m1} & a_{m2} & \dots & a_{mn}
\end{pmatrix}
$$
と書きます。各 $a_{ij}$ を 成分 といいます。
(2) 行と列
$i$ 行目は $(a_{i1},\dots,a_{in})$，$j$ 列目は $\begin{pmatrix} a_{1j} \\ \vdots, \\ a_{mj} \end{pmatrix}$です。
行は横方向の並び，列は縦方向の並びを表します。
(3) 行ベクトルと列ベクトル
列ベクトルとは 1 列だけを持つ $m\times 1$ 行列：$\displaystyle \mathbf{x}=\begin{pmatrix}x_1\\ \vdots\\ x_m\end{pmatrix}$のことです。
行ベクトルとは 1 行だけを持つ $1\times n$ 行列：$\displaystyle \mathbf{y}=\begin{pmatrix}y_1&\dots&y_n\end{pmatrix}$のことです。
2. 色々な行列
(1) 正方行列の定義
行と列の数が等しい $n\times n$ 行列を 正方行列 といいます。
(2) 対角行列の定義
非対角成分がすべて $0$ の正方行列を対角行列といいます。
$$
\mathrm{diag}(d_1,\dots,d_n)=
\begin{pmatrix}
d_1 & 0 & \dots & 0\\
0 & d_2 & \dots & 0\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \dots & d_n
\end{pmatrix}.
$$
(3) 三角行列の定義
- 主対角線より下が $0$の行列を上三角行列といいます。
- 主対角線より上が $0$の行列を下三角行列といいます。
(4) 単位行列の定義
主対角がすべて $1$ の正方行列を 単位行列 $I_n$ といいます。任意の $n\times n$ 行列 $A$ に対し $I_nA=AI_n=A$が成り立ちます。
(5) ゼロ行列の定義
全成分が $0$ の行列を ゼロ行列（$O$ または $0_{m\times n}$）といいます。
3. 行列の和とスカラー倍
(1) 行列の和と差
$A,B$ が同じサイズ $m\times n$ のときのみ $A\pm B$ が定義され、成分同士の和または差$(A\pm B)_{ij}=a_{ij}\pm b_{ij}$で与えられます。
(2) 行列の和と差の性質
交換法則
$A+B=B+A$
証明をみる
成分ごとに $a_{ij}+b_{ij}=b_{ij}+a_{ij}$（実数の交換法則）より成り立つ。結合法則
$(A+B)+C=A+(B+C)$
証明をみる
$((A+B)+C)_{ij}=(a_{ij}+b_{ij})+c_{ij}=a_{ij}+(b_{ij}+c_{ij})=(A+(B+C))_{ij}$（実数の結合法則）。よって両辺の全成分が一致。$\square$(3) 行列のスカラー倍
成分のスカラー倍$(\alpha A)_{ij}=\alpha a_{ij}$で定義されます。
(4) 行列のスカラー倍の性質
線形性(1)
$(\alpha+\beta)A=\alpha A+\beta A$
証明をみる
$((\alpha+\beta)A)_{ij}=(\alpha+\beta)a_{ij}=\alpha a_{ij}+\beta a_{ij}=(\alpha A+\beta A)_{ij}$。線形性(2)
$\alpha(A+B)=\alpha A+\alpha B$
証明をみる
左辺 $(\alpha(A+B))_{ij}=\alpha(a_{ij}+b_{ij})=\alpha a_{ij}+\alpha b_{ij}=(\alpha A+\alpha B)_{ij}$。$\square$4. 行列の積
(1) 行列の積
行列$A, B$の積$AB$は$A$の列数と$B$の行数が等しいときのみ定義されます。
具体的には、$m\times n$ 行列 $A=(a_{ik})$ と $n\times p$ 行列 $B=(b_{kj})$ の積 $C=AB$ は $m\times p$ 行列で以下で与えられます。
$$c_{ij}=\sum_{k=1}^n a_{ik}b_{kj}.$$
(2) 行列の積の定義の理由・背景
線形写像 $T:\mathbb{R}^n\to\mathbb{R}^m$，$S:\mathbb{R}^p\to\mathbb{R}^n$ の合成 $T\circ S:\mathbb{R}^p\to\mathbb{R}^m$ に対し，標準基底に関する行列表現を $A,B$ とすると，合成の行列は $AB$ になります。実際，任意のベクトル $\mathbf{x}\in\mathbb{R}^p$ について
$$T(S(\mathbf{x}))=A(B\mathbf{x})=(AB)\mathbf{x},$$
が成分定義と一致するよう積が定められています。
線型写像については以下の記事を参照して下さい。
証明をみる (成分を用いた証明)
行列 $A$ を $m\times n$、行列 $B$ を $n\times p$ とし、積 $C=AB$ は $m\times p$ 行列とする。線形写像の合成式 $$ A(B\mathbf{x})=(AB)\mathbf{x} $$ を用いて、$C$ の成分 $c_{ij}$ が $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj} $$ で与えられることを示す。$\mathbf{x}\in\mathbb{R}^p$ を任意の列ベクトルとする。まず $B\mathbf{x}$ の第 $k$ 成分は $$ (B\mathbf{x})_k=\sum_{j=1}^{p}b_{kj}x_j. $$ 次に $A(B\mathbf{x})$ の第 $i$ 成分は $$ \bigl(A(B\mathbf{x})\bigr)_i=\sum_{k=1}^{n}a_{ik}(B\mathbf{x})_k=\sum_{k=1}^{n}a_{ik}\left(\sum_{j=1}^{p}b_{kj}x_j\right)=\sum_{j=1}^{p}\left(\sum_{k=1}^{n}a_{ik}b_{kj}\right)x_j. $$ 一方で、$C=AB$ とおいたとき $(C\mathbf{x})_i$ は $$ (C\mathbf{x})_i=\sum_{j=1}^{p}c_{ij}x_j. $$ 合成の等式 $A(B\mathbf{x})=(AB)\mathbf{x}=C\mathbf{x}$ より、任意の $\mathbf{x}$ に対して $$ \sum_{j=1}^{p}\left(\sum_{k=1}^{n}a_{ik}b_{kj}\right)x_j=\sum_{j=1}^{p}c_{ij}x_j $$ が成り立つ。これは全ての $x_j$ に対して成り立つ恒等式なので、各係数が一致しなければならない。ゆえに $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj}\qquad(1\le i\le m,\ 1\le j\le p). $$
証明をみる (標準基底ベクトルの像を用いる証明)
行列 $A$ を $m\times n$、行列 $B$ を $n\times p$ とし、積 $C=AB$ は $m\times p$ 行列とする。線形写像の合成式 $$ A(B\mathbf{x})=(AB)\mathbf{x} $$ を用いて、$C$ の成分 $c_{ij}$ が $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj} $$ で与えられることを示す。$\mathbf{e}_j\in\mathbb{R}^p$ を第 $j$ 成分のみ $1$、他は $0$ の標準基底とする。$B\mathbf{e}_j$ は $B$ の第 $j$ 列で、その第 $k$ 成分は $b_{kj}$ である。よって $$ A(B\mathbf{e}_j)=A\begin{pmatrix}b_{1j}\\ \vdots\\ b_{nj}\end{pmatrix} $$ の第 $i$ 成分は $$ \sum_{k=1}^{n}a_{ik}b_{kj}. $$ 一方、$A(B\mathbf{e}_j)=(AB)\mathbf{e}_j=C\mathbf{e}_j$ は $C$ の第 $j$ 列であり、その第 $i$ 成分は $c_{ij}$。したがって $$ c_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj}. $$ 以上で、線形写像の合成 $A(B\mathbf{x})=(AB)\mathbf{x}$ から、行列積の成分表示 $$ (AB)_{ij}=\sum_{k=1}^{n}a_{ik}b_{kj} $$ が導かれた。□
規定については以下の記事を参照して下さい。
証明をみる (ベクトルの内積から構築)
以下のように考えると積の定義が自然であることが分かります。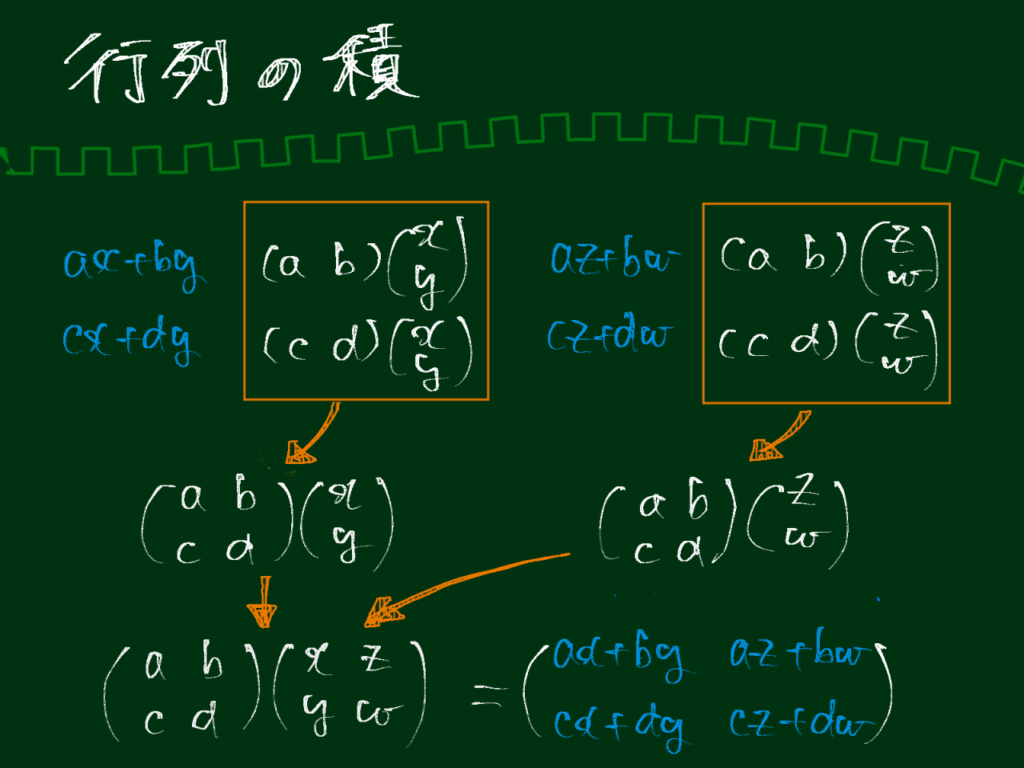
(3) 行列の積の性質
結合法則
適合するサイズで $(AB)C=A(BC)$
証明をみる
成分で $$ \big((AB)C\big)_{ij}=\sum{k}(AB)_{ik}c_{kj}=\sum_k\left(\sum_{\ell}a_{i\ell}b_{\ell k}\right)c_{kj} =\sum_{\ell}a_{i\ell}\left(\sum_k b_{\ell k}c_{kj}\right) =\big(A(BC)\big)_{ij}. $$ 有限和なので和の順序交換が正当化される。よって全成分が一致する。$\square$分配法則
$A(B+C)=AB+AC$
証明をみる
成分で $$(A(B+C))_{ij}=\sum_k a_{ik}(b_{kj}+c_{kj})=\sum_k a_{ik}b_{kj}+\sum_k a_{ik}c_{kj}=(AB+AC)_{ij}.$$ 同様に $(A+B)C=AC+BC$。$\square$交換法則は不成立
一般に $AB\neq BA$
証明をみる
例えば $$ A=\begin{pmatrix}0&1\\0&0\end{pmatrix},\quad B=\begin{pmatrix}0&0\\1&0\end{pmatrix} $$ では $$ AB=\begin{pmatrix}1&0\\0&0\end{pmatrix},\quad BA=\begin{pmatrix}0&0\\0&1\end{pmatrix}, $$ と一致しません。$\square$(4) 行列の積をブロックに分けて計算する方法
行列の積は小行列（ブロック）に分割し、それに対して積の定義を適用して計算することができます。
例えば
$$
A = \begin{pmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{pmatrix},\quad
B = \begin{pmatrix} B_{11} & B_{12} \\ B_{21} & B_{22} \end{pmatrix}
$$
と $2\times 2$ ブロックに分けられるとき、
$$
AB = \begin{pmatrix}
A_{11}B_{11} + A_{12}B_{21} & A_{11}B_{12} + A_{12}B_{22} \\
A_{21}B_{11} + A_{22}B_{21} & A_{21}B_{12} + A_{22}B_{22}
\end{pmatrix}
$$
となります。
イメージは以下です。
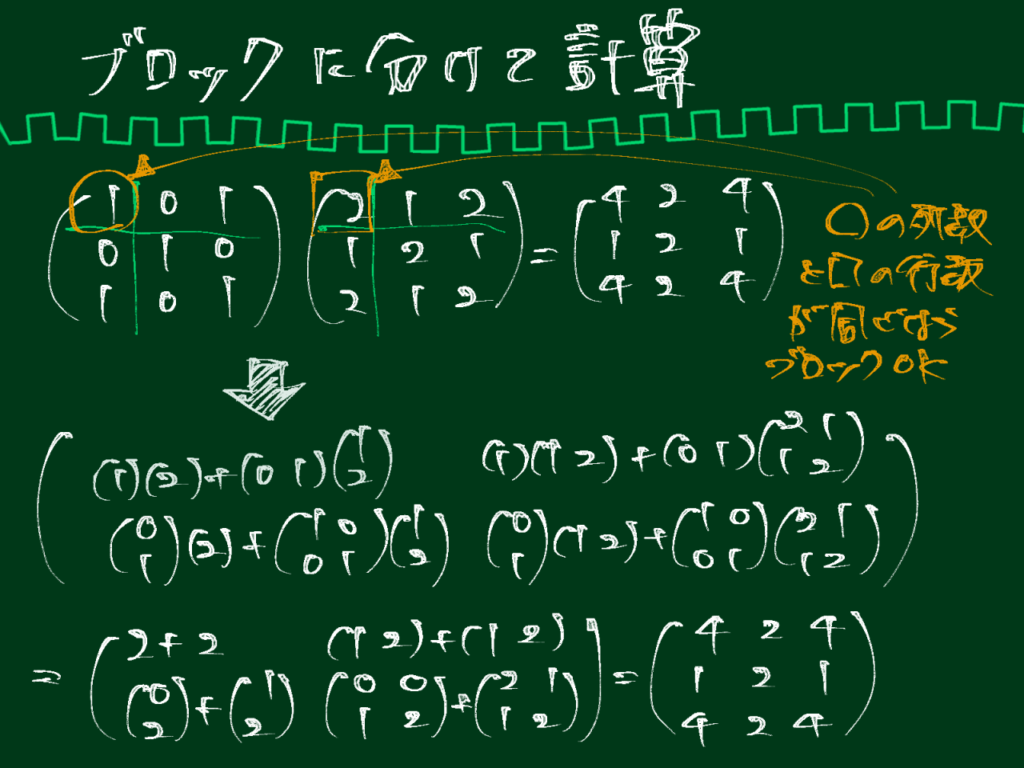
なお、ブロックによる行列の計算では、以下の点について銘記しておくと良いです。
- ブロックのサイズが噛み合っていること（掛ける内側の次元が一致）を必ず確認する。
例：$A_{12}$（$3\times2$）と $B_{21}$（$2\times2$）は掛けられるが、もし $B_{21}$ が $3\times2$ なら掛けられません。 - ゼロブロック・対角ブロック・三角ブロックがあるときは、不要な計算を省ける（効率化）。
- 理解のコツは「ブロックも行列、だからブロック同士で普通の行列積をする」。最後に同じ位置のブロックを足すだけです。
以下に実際の計算例を2つ掲載します。
具体例をみる: $4\times4$を$2\times2$のブロックにする例
$4\times4$ 行列を $2\times2$ ブロック（各ブロックは $2\times2$）に分けます。 $$ A=\begin{pmatrix} \boxed{\begin{matrix}1&2\\3&4\end{matrix}}&\boxed{\begin{matrix}5&6\\7&8\end{matrix}}\\[6pt] \boxed{\begin{matrix}0&1\\2&3\end{matrix}}&\boxed{\begin{matrix}4&0\\1&2\end{matrix}} \end{pmatrix} = \begin{pmatrix}A_{11}&A_{12}\\A_{21}&A_{22}\end{pmatrix}, \quad B=\begin{pmatrix} \boxed{\begin{matrix}2&1\\0&1\end{matrix}}&\boxed{\begin{matrix}3&0\\1&2\end{matrix}}\\[6pt] \boxed{\begin{matrix}1&4\\2&0\end{matrix}}&\boxed{\begin{matrix}0&5\\2&1\end{matrix}} \end{pmatrix} = \begin{pmatrix}B_{11}&B_{12}\\B_{21}&B_{22}\end{pmatrix}. $$(1) 上左ブロック $C_{11}=A_{11}B_{11}+A_{12}B_{21}$
$$ A_{11}B_{11}=\begin{pmatrix}1&2\\3&4\end{pmatrix}\begin{pmatrix}2&1\\0&1\end{pmatrix} =\begin{pmatrix} 1\cdot2+2\cdot0&1\cdot1+2\cdot1\\ 3\cdot2+4\cdot0&3\cdot1+4\cdot1 \end{pmatrix} =\begin{pmatrix}2&3\\6&7\end{pmatrix} $$ $$ A_{12}B_{21}=\begin{pmatrix}5&6\\7&8\end{pmatrix}\begin{pmatrix}1&4\\2&0\end{pmatrix} =\begin{pmatrix} 5\cdot1+6\cdot2&5\cdot4+6\cdot0\\ 7\cdot1+8\cdot2&7\cdot4+8\cdot0 \end{pmatrix} =\begin{pmatrix}17&20\\23&28\end{pmatrix} $$ $$ C_{11}=A_{11}B_{11}+A_{12}B_{21} =\begin{pmatrix}2&3\\6&7\end{pmatrix}+\begin{pmatrix}17&20\\23&28\end{pmatrix} =\begin{pmatrix}19&23\\29&35\end{pmatrix} $$
(2) 上右ブロック $C_{12}=A_{11}B_{12}+A_{12}B_{22}$
$$ A_{11}B_{12}=\begin{pmatrix}1&2\\3&4\end{pmatrix}\begin{pmatrix}3&0\\1&2\end{pmatrix} =\begin{pmatrix} 1\cdot3+2\cdot1&1\cdot0+2\cdot2\\ 3\cdot3+4\cdot1&3\cdot0+4\cdot2 \end{pmatrix} =\begin{pmatrix}5&4\\13&8\end{pmatrix} $$ $$ A_{12}B_{22}=\begin{pmatrix}5&6\\7&8\end{pmatrix}\begin{pmatrix}0&5\\2&1\end{pmatrix} =\begin{pmatrix} 5\cdot0+6\cdot2&5\cdot5+6\cdot1\\ 7\cdot0+8\cdot2&7\cdot5+8\cdot1 \end{pmatrix} =\begin{pmatrix}12&31\\16&43\end{pmatrix} $$ $$ C_{12}=\begin{pmatrix}5&4\\13&8\end{pmatrix}+\begin{pmatrix}12&31\\16&43\end{pmatrix} =\begin{pmatrix}17&35\\29&51\end{pmatrix} $$
(3) 下左ブロック $C_{21}=A_{21}B_{11}+A_{22}B_{21}$
$$ A_{21}B_{11}=\begin{pmatrix}0&1\\2&3\end{pmatrix}\begin{pmatrix}2&1\\0&1\end{pmatrix} =\begin{pmatrix} 0\cdot2+1\cdot0&0\cdot1+1\cdot1\\ 2\cdot2+3\cdot0&2\cdot1+3\cdot1 \end{pmatrix} =\begin{pmatrix}0&1\\4&5\end{pmatrix} $$ $$ A_{22}B_{21}=\begin{pmatrix}4&0\\1&2\end{pmatrix}\begin{pmatrix}1&4\\2&0\end{pmatrix} =\begin{pmatrix} 4\cdot1+0\cdot2&4\cdot4+0\cdot0\\ 1\cdot1+2\cdot2&1\cdot4+2\cdot0 \end{pmatrix} =\begin{pmatrix}4&16\\5&4\end{pmatrix} $$ $$ C_{21}=\begin{pmatrix}0&1\\4&5\end{pmatrix}+\begin{pmatrix}4&16\\5&4\end{pmatrix} =\begin{pmatrix}4&17\\9&9\end{pmatrix} $$
(4) 下右ブロック $C_{22}=A_{21}B_{12}+A_{22}B_{22}$
$$ A_{21}B_{12}=\begin{pmatrix}0&1\\2&3\end{pmatrix}\begin{pmatrix}3&0\\1&2\end{pmatrix} =\begin{pmatrix} 0\cdot3+1\cdot1&0\cdot0+1\cdot2\\ 2\cdot3+3\cdot1&2\cdot0+3\cdot2 \end{pmatrix} =\begin{pmatrix}1&2\\9&6\end{pmatrix} $$ $$ A_{22}B_{22}=\begin{pmatrix}4&0\\1&2\end{pmatrix}\begin{pmatrix}0&5\\2&1\end{pmatrix} =\begin{pmatrix} 4\cdot0+0\cdot2&4\cdot5+0\cdot1\\ 1\cdot0+2\cdot2&1\cdot5+2\cdot1 \end{pmatrix} =\begin{pmatrix}0&20\\4&7\end{pmatrix} $$ $$ C_{22}=\begin{pmatrix}1&2\\9&6\end{pmatrix}+\begin{pmatrix}0&20\\4&7\end{pmatrix} =\begin{pmatrix}1&22\\13&13\end{pmatrix} $$
(5) 組み立て（$C=AB$）
$$ C=\begin{pmatrix} \boxed{C_{11}}&\boxed{C_{12}}\\ \boxed{C_{21}}&\boxed{C_{22}} \end{pmatrix} = \begin{pmatrix} 19&23&17&35\\ 29&35&29&51\\ 4&17&1&22\\ 9&9&13&13 \end{pmatrix} $$
具体例をみる: 長方形ブロック（行列サイズが違う場合）の例
$A$ が $3\times4$、$B$ が $4\times2$とし、列方向／行方向に分割して $$ A=\bigl[A_{11}\ \ A_{12}\bigr],\quad A_{11}\in\mathbb{R}^{3\times2},\ A_{12}\in\mathbb{R}^{3\times2} $$ $$ B=\begin{bmatrix}B_{11}\\ B_{21}\end{bmatrix},\quad B_{11}\in\mathbb{R}^{2\times2},\ B_{21}\in\mathbb{R}^{2\times2} $$ このとき $$ AB=A_{11}B_{11}+A_{12}B_{21}\quad(\text{サイズ }3\times2) $$具体的に
$$ A=\begin{pmatrix} 1&2&3&4\\ 0&1&0&1\\ 2&0&1&0 \end{pmatrix}, \quad B=\begin{pmatrix} 1&0\\ 2&1\\ 0&1\\ 3&2 \end{pmatrix} $$ とし、前半2列・後半2列で分ける： $$ A_{11}=\begin{pmatrix}1&2\\0&1\\2&0\end{pmatrix},\quad A_{12}=\begin{pmatrix}3&4\\0&1\\1&0\end{pmatrix} $$ $$ B_{11}=\begin{pmatrix}1&0\\2&1\end{pmatrix},\quad B_{21}=\begin{pmatrix}0&1\\3&2\end{pmatrix} $$
(1) 各ブロックの積
$$ A_{11}B_{11}= \begin{pmatrix}1&2\\0&1\\2&0\end{pmatrix} \begin{pmatrix}1&0\\2&1\end{pmatrix} = \begin{pmatrix} 1\cdot1+2\cdot2&1\cdot0+2\cdot1\\ 0\cdot1+1\cdot2&0\cdot0+1\cdot1\\ 2\cdot1+0\cdot2&2\cdot0+0\cdot1 \end{pmatrix} = \begin{pmatrix}5&2\\2&1\\2&0\end{pmatrix} $$ $$ A_{12}B_{21}= \begin{pmatrix}3&4\\0&1\\1&0\end{pmatrix} \begin{pmatrix}0&1\\3&2\end{pmatrix} = \begin{pmatrix} 3\cdot0+4\cdot3&3\cdot1+4\cdot2\\ 0\cdot0+1\cdot3&0\cdot1+1\cdot2\\ 1\cdot0+0\cdot3&1\cdot1+0\cdot2 \end{pmatrix} = \begin{pmatrix}12&11\\3&2\\0&1\end{pmatrix} $$
(2) 和をとって $AB$
$$ AB=A_{11}B_{11}+A_{12}B_{21} =\begin{pmatrix}5&2\\2&1\\2&0\end{pmatrix} +\begin{pmatrix}12&11\\3&2\\0&1\end{pmatrix} = \begin{pmatrix}17&13\\5&3\\2&1\end{pmatrix} $$
(3) 直接計算での検算（任意）
$$ AB= \begin{pmatrix} 1&2&3&4\\ 0&1&0&1\\ 2&0&1&0 \end{pmatrix} \begin{pmatrix} 1&0\\ 2&1\\ 0&1\\ 3&2 \end{pmatrix} = \begin{pmatrix} 1\cdot1+2\cdot2+3\cdot0+4\cdot3&1\cdot0+2\cdot1+3\cdot1+4\cdot2\\ 0\cdot1+1\cdot2+0\cdot0+1\cdot3&0\cdot0+1\cdot1+0\cdot1+1\cdot2\\ 2\cdot1+0\cdot2+1\cdot0+0\cdot3&2\cdot0+0\cdot1+1\cdot1+0\cdot2 \end{pmatrix} = \begin{pmatrix}17&13\\5&3\\2&1\end{pmatrix} $$ 一致していることが確認できます。
5. 行列の積に関する色々な行列
(1) ゼロ因子
ゼロ因子
$A\neq O,\ B\neq O$ だが $AB=O$ となるとき，$A,B$ を零因子という。
具体例をみる
$$ A=\begin{pmatrix}1&0\\0&0\end{pmatrix},\quad B=\begin{pmatrix}0&0\\1&0\end{pmatrix}\quad\Rightarrow\quad AB=O. $$(2) べき零行列（ニルポテント）
べき零行列（ニルポテント）
ある $k\in\mathbb{N}$ で $A^k=O$となる行列をべき零行列という。
具体例をみる
$N=\begin{pmatrix}0&1\\0&0\end{pmatrix}$ は $N^2=O$。(3) べき等行列（イドポテント）
べき等行列（イドポテント）
$P^2=P$となる行列をべき等行列という。
具体例をみる
$P=\begin{pmatrix}1&0\\0&0\end{pmatrix}$ は $P^2=P$。6. 行列の積に戻す公式
以下の3つの変形は頻出するので、覚えておくと便利です。
右辺の積を計算することで左辺が得られ、簡単に証明ができます。
(1) $a\mathbf{x}+b\mathbf{y}+c\mathbf{z}$ の行列表現
$$
a\mathbf{x}+b\mathbf{y}+c\mathbf{z}=(\mathbf{x}\ \mathbf{y}\ \mathbf{z})\begin{pmatrix}a\\b\\c\end{pmatrix}.
$$
(2) $(a\mathbf{x},\,b\mathbf{y},\,c\mathbf{z})$ の行列表現
$$
(a\mathbf{x}\ \ b\mathbf{y}\ \ c\mathbf{z})=(\mathbf{x}\ \mathbf{y}\ \ \mathbf{z})\,\mathrm{diag}(a,b,c).
$$
(3) $(a\mathbf{x},\,\mathbf{x}+b\mathbf{y},\,\mathbf{y}+c\mathbf{z})$ の行列表現
$$
(a\mathbf{x}\ \ \mathbf{x}+b\mathbf{y}\ \ \mathbf{y}+c\mathbf{z})
=(\mathbf{x}\ \mathbf{y}\ \mathbf{z})
\begin{pmatrix}
a&1&0\\
0&b&1\\
0&0&c
\end{pmatrix}.
$$
(4) まとめ
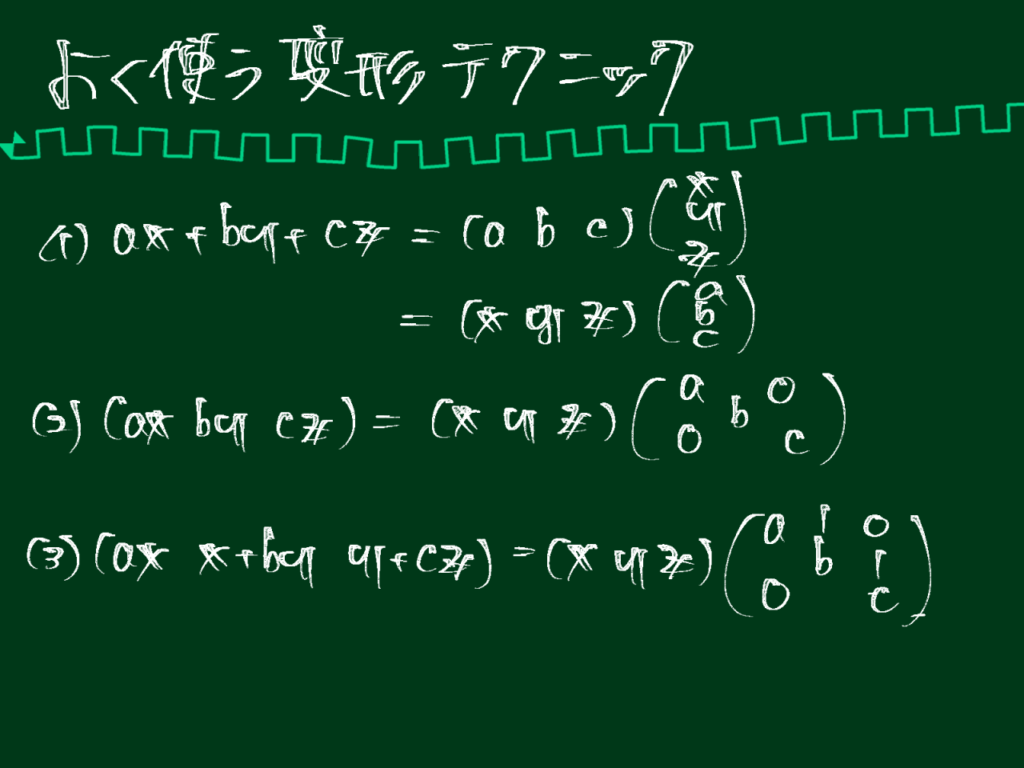
7. 行列式
複数の方程式をまとめた行列による方程式について、各々の方程式を解かずに行列のまま解くことができれば計算が楽になります。
そのためには$AA^{-1}=A^{-1}A=I$となる逆行列$A^{-1}$という概念を導入します。
これで$AX=B$のような方程式については両辺に左から$A^{-1}$をかけて$X=A^{-1}B$として解くことができます。
逆行列は行列式という概念を用いて定義されるため、本節では行列式について説明をします。
ただし本節では2次または3次の正方行列の行列式を具体的に紹介するにとどめ、n次正方行列に対する詳しい行列式の定義や説明は以下の記事に譲ります。
(1) 行列式の定義
以下の定義の意味は上記で紹介した「行列式」の記事で詳細を説明しています。本節では参考程度に載せており、現段階では無理に理解する必要はありません。
行列式の定義
$n\times n$ 行列 $A=(a_{ij})$ の行列式$\det A$または$|A|$は
$$
\det(A)=\sum_{\sigma\in S_n}\operatorname{sgn}(\sigma)\prod_{i=1}^n a_{i,\sigma(i)}.
$$
ここで $S_n$ は $n$ 元対称群，$\operatorname{sgn}(\sigma)\in{+1,-1}$ は置換の符号。
(2) 2次正方行列の行列式
2次正方行列の行列式の公式
2次正方行列の行列式の公式は以下。
$$
\det\begin{pmatrix}a&b\\ c&d\end{pmatrix}
=ad-bc.
$$
証明をみる
2次正方行列の公式は以下のように導出できる。 $$ \det\begin{pmatrix}a&b\\ c&d\end{pmatrix} =\operatorname{sgn}(\mathrm{id})\,a d+\operatorname{sgn}((12))\,b c=ad-bc. $$ （$S_2={\mathrm{id},(12)}$，後者は奇置換で符号 $-$。）$\square$具体例をみる
次の 2 次正方行列を考えます。 $$ A=\begin{pmatrix} 3&-2\\ 5&4 \end{pmatrix} $$ 2×2 行列の行列式の公式は $$ \det\begin{pmatrix} a&b\\ c&d \end{pmatrix}=ad-bc $$ です。これを $A$ に適用すると，$a=3,\ b=-2,\ c=5,\ d=4$ なので1. 斜めの積を計算： $$ ad=3\cdot4=12,\qquad bc=(-2)\cdot5=-10 $$
2. 差をとる（$ad-bc$）： $$ \det A=12-(-10)=12+10=22 $$
**結論**： $$ \boxed{\det A=22} $$
(3) 3次正方行列の行列式
3次正方行列の行列式の公式(サラスの公式)
3次正方行列の行列式は以下で与えられます。
$$
\det\begin{pmatrix}a&b&c\\ d&e&f\\ g&h&i\end{pmatrix}
=aei+bfg+cdh-ceg-bdi-afh.
$$
以下にイメージも載せておきます。
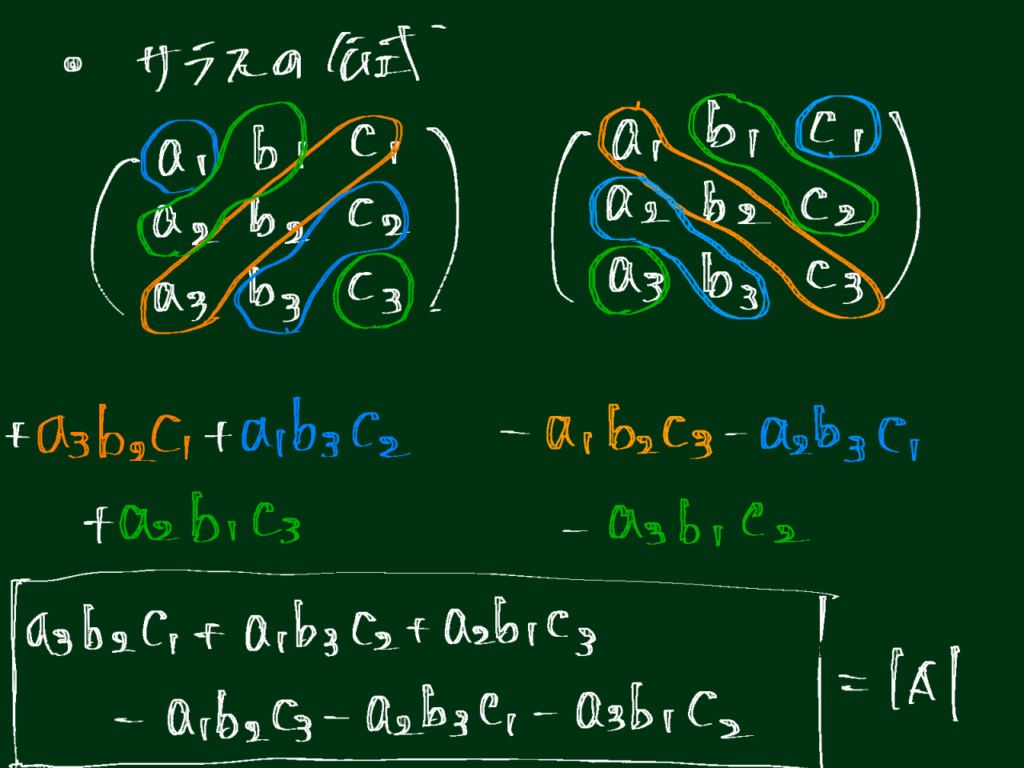
証明をみる
1行目で余因子展開（ラプラス展開）すると $$ \det A =a\begin{vmatrix}e&f\\h&i\end{vmatrix} -b\begin{vmatrix}d&f\\g&i\end{vmatrix} +c\begin{vmatrix}d&e\\g&h\end{vmatrix}. $$ 各 $2\times2$ 行列式を計算すると $$ \begin{vmatrix}e&f\\h&i\end{vmatrix}=ei-fh,\qquad \begin{vmatrix}d&f\\g&i\end{vmatrix}=di-fg,\qquad \begin{vmatrix}d&e\\g&h\end{vmatrix}=dh-eg. $$ したがって $$ \det A =a(ei-fh)-b(di-fg)+c(dh-eg). $$ 右辺を展開・整理すると $$ \det A =aei-afh-bdi+bfg+cdh-ceg. $$ 並べ替えると $$ \det A =\underbrace{aei+bfg+cdh}_{\text{正の和}} -\underbrace{(ceg+bdi+afh)}_{\text{負の和}}. $$ これがサラスの公式そのものである。□余因子展開については以下の記事を参照して下さい。
具体例をみる
次の 3 次正方行列を考えます。 $$ A=\begin{pmatrix} 2 & 3 & 1 \\ 4 & 1 & -2 \\ -1 & 5 & 3 \end{pmatrix} $$1. **最初の 2 列を右に書き足す**
$$ \begin{array}{ccc|cc} 2 & 3 & 1 & 2 & 3 \\ 4 & 1 & -2 & 4 & 1 \\ -1 & 5 & 3 & -1 & 5 \end{array} $$
2. **左上から右下への3本の対角線の積の和を求める**
– 1本目：$2 \times 1 \times 3 = 6$
– 2本目：$3 \times (-2) \times (-1) = 6$
– 3本目：$1 \times 4 \times 5 = 20$
和： $$ 6 + 6 + 20 = 32 $$
3. **右上から左下への3本の対角線の積の和を求める**
– 1本目：$1 \times 1 \times (-1) = -1$
– 2本目：$2 \times (-2) \times 5 = -20$
– 3本目：$3 \times 4 \times 3 = 36$
和： $$ -1 + (-20) + 36 = 15 $$
4. **差をとる（右下方向の和 − 左下方向の和）** $$ \det A = 32 – 15 = 17 $$
**結論**： $$ \boxed{\det A = 17} $$
8. 逆行列
逆行列は行列で表現した方程式をそのまま解く際などに用います。これにより、行列としてまとめる前の個々の方程式を個別に解かずに一括して解くことができるようになります。
(1) 逆行列
逆行列の定義
正方行列 $A$の逆行列は$AB=BA=I$を満たす$B$のことで$B=A^{-1}$と表記する。
(2) 正則
正則の定義
正方行列 $A$ が 正則 とは，$A^{-1}$ が存在し $AA^{-1}=A^{-1}A=I$ を満たすこと。
(3) 余因子
余因子は一般の行列式の計算や逆行列の計算に用いる概念であり「行列式」の記事で詳しく解説しています。定義の背景などはそちらを参考にし、本節では定義のみ掲載しておきます。
余因子の定義
$C_{ij}=(-1)^{i+j}M_{ij}$（$M_{ij}$ は $i$ 行 $j$ 列を除いた小行列の行列式）を余因子という。
(4) 余因子行列
余因子行列は逆行列の定義や計算に用いる概念であり「行列式」の記事で詳しく解説しています。定義の背景などはそちらを参考にし、本節では定義のみ掲載しておきます。
余因子 $C_{ij}=(-1)^{i+j}M_{ij}$ を並べた行列 $C=(C_{ij})$ の転置
$$\operatorname{adj}(A)=C^T$$
を 余因子行列 という。
(5) 余因子行列の基本恒等式
余因子行列の基本恒等式は余因子行列によって逆行列を表すために用いる定理です。「行列式」の記事で詳しく解説しています。定義の背景などはそちらを参考にし、本節では定義のみ掲載しておきます。
余因子行列の基本恒等式
余因子行列について、以下の基本恒等式が成立する。
$A\,\operatorname{adj}(A)=\operatorname{adj}(A)\,A=\det(A)\,I$
証明をみる
$(A\,\operatorname{adj}(A)){ij}=\sum{k=1}^n a_{ik}C_{jk}$ である。 $i=j$ のとき：$\displaystyle \sum_k a_{ik}C_{ik}$ は $i$ 行に沿う余因子展開そのもので $\det(A)$。 $i\neq j$ のとき：$A$ の 第 $i$ 行を第 $j$ 行に置き換えた行列 を $A’$ とすると 2 行が等しく $\det(A’)=0$。一方，$\det(A’)$ を第 $j$ 行に沿って展開すると $$ \det(A’)=\sum_k a_{ik}C_{jk}=(A\,\operatorname{adj}(A))_{ij}. $$ よって $(A\,\operatorname{adj}(A)){ij}=0$。 以上から $$ A\,\operatorname{adj}(A)=\det(A)\,I. $$ 右側乗でも同様に示せる。$\square$(6) 逆行列の余因子行列による表現
余因子行列を利用して逆行列を求めることができます。詳しくは「行列式」の記事で詳しく解説しています。詳しい証明などはそちらを参考にし、本節では結論と簡単な証明のみ掲載しておきます。
逆行列の余因子行列による表現
基本恒等式を用いると、以下のように逆行列を与えることができる。
$\det(A)\neq 0$ なら
$$
\boxed{\ A^{-1}=\frac{1}{\det(A)}\,\operatorname{adj}(A)\ }.
$$
(6) 2次正方行列の逆行列の公式
2次正方行列の逆行列の公式
2次正方行列の逆行列は以下。
$$A^{-1}=\frac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}.$$
証明をみる
$A$ の $(i,j)$ 成分の**余因子** $C_{ij}$ を $$ C_{ij}=(-1)^{i+j}M_{ij}, $$ ここで $M_{ij}$ は $A$ の第 $i$ 行第 $j$ 列を除いた小行列（$2\times2$ の場合は $1\times1$）の行列式とする。 $2\times2$ のときは $$ M_{11}=d,\quad M_{12}=c,\quad M_{21}=b,\quad M_{22}=a, $$ したがって $$ C_{11}=d,\quad C_{12}=-c,\quad C_{21}=-b,\quad C_{22}=a. $$ **余因子行列**（cofactor matrix）は $$ C=\begin{pmatrix}C_{11}&C_{12}\\C_{21}&C_{22}\end{pmatrix} =\begin{pmatrix}d&-c\\-b&a\end{pmatrix}, $$ **随伴行列**（adjugate，adjoint）はその転置 $$ \operatorname{adj}(A)=C^{\mathsf T} =\begin{pmatrix}d&-b\\-c&a\end{pmatrix}. $$次に、以下の恒等式を2×2 で直接計算して確かめる。 $$ A\,\operatorname{adj}(A)=\det(A)\,I. $$ 左辺を成分計算すると $$ A\,\operatorname{adj}(A) =\begin{pmatrix}a&b\\c&d\end{pmatrix} \begin{pmatrix}d&-b\\-c&a\end{pmatrix} =\begin{pmatrix} ad-bc&-ab+ab\\ cd-dc&-bc+ad \end{pmatrix} =\begin{pmatrix} ad-bc&0\\ 0&ad-bc \end{pmatrix} =(ad-bc)I. $$ 右辺は $\det(A)\,I=(ad-bc)I$ なので一致する。
従って、$\det(A)\neq0$ ならば，上の恒等式の両辺を $\det(A)$ で割って $$ A\left(\frac{1}{\det(A)}\operatorname{adj}(A)\right)=I $$ が得られる。よって $$ A^{-1}=\frac{1}{\det(A)}\operatorname{adj}(A). $$
2×2 では具体的に $$ \det(A)=ad-bc,\qquad \operatorname{adj}(A)=\begin{pmatrix}d&-b\\-c&a\end{pmatrix} $$ だから $$ \boxed{\; A^{-1}=\frac{1}{ad-bc}\begin{pmatrix}d&-b\\-c&a\end{pmatrix}\; } $$
9. 転置
(1) 転置行列
転置と転置行列
$A=(a_{ij})$ の 転置 は $A^T=(a_{ji})$。行と列を入れ替える操作。
また、$A^T$を$A$の転置行列という。
また、$A^T$を$A$の転置行列という。
(2) 随伴行列
随伴行列
複素数体上では随伴（共役転置） を $A^*=\overline{A}^T$ と定める（実行列なら $A^*=A^T$）。
また、$A^*$を$A$の随伴行列という。
また、$A^*$を$A$の随伴行列という。
10. 転置に関する公式
(1) 積の転置
積の転置
$(AB)^T=B^TA^T$
証明をみる
成分で $$ (AB)^T_{ij}=(AB)_{ji}=\sum_k a{jk}b_{ki}=\sum_k b_{ki}a_{jk}=(B^TA^T)_{ij}. \square $$(2) 逆行列の転置
逆行列の転置
$(A^{-1})^T=(A^T)^{-1}$
証明をみる
$AA^{-1}=I$ を転置して $(A^{-1})^TA^T=I$。$\square$(3) 転置行列の行列式
$\det(A^T)=\det(A)$
証明をみる
置換定義は行版・列版で同値，あるいは余因子展開を行方向・列方向いずれでしても値は同じ。$\square$置換や余因子展開については以下の記事を参照。
11. トレース
(1) 定義
トレースの定義
正方行列 $A=(a_{ij})$ の トレース は主対角の和：
$$\operatorname{tr}(A)=\sum_{i=1}^n a_{ii}.$$
(2) 積のトレースの循環性
積のトレースの循環性
トレースについて以下の2式が成立する。
$$\operatorname{tr}(AB)=\operatorname{tr}(BA)$$
$$\operatorname{tr}(ABC)=\operatorname{tr}(BCA)=\operatorname{tr}(CAB)$$
証明をみる
$$ \operatorname{tr}(AB)=\sum_{i}(AB)_{ii} =\sum_i\sum_j a_{ij}b_{ji} =\sum_j\sum_i b_{ji}a_{ij} =\sum_j(BA)_{jj} =\operatorname{tr}(BA). $$ 有限和なので順序交換が正当化される。さらに同様の帰納で $\operatorname{tr}(ABC)=\operatorname{tr}(BCA)=\operatorname{tr}(CAB)$ も成り立つ。$\square$(3) 自身の転置との積（フロベニウスノルム）
フロベニウスノルム
$\langle A,B\rangle_F=\operatorname{tr}(A^TB)$をフロベニウス内積といい、以下が成立する。
$$
\langle A,A\rangle_F = \operatorname{tr}(A^TA)=\sum_{i,j} a_{ij}^2
$$
証明をみる
$$ \operatorname{tr}(A^TA)=\sum_i (A^TA)_{ii} =\sum_i\sum_j a_{ji}a_{ji} =\sum_{i,j} a_{ij}^2. $$ 右辺はフロベニウスノルム $|A|_F^2$。$\square$(4) 2次形式のトレース
2次形式のトレース
列ベクトル $\mathbf{x}\in\mathbb{R}^n$ に対して
$$\mathbf{x}^TA\mathbf{x}=\operatorname{tr}\big(A\,\mathbf{x}\mathbf{x}^T\big)$$
コメント