行列式は逆行列の計算に必要な概念です。逆行列は複数の方程式をまとめた行列の方程式を解くために必要な概念です。
2次や3次の正方行列の行列式は以下の第3章の定義3.19でも扱いましたが、本章では$n$次の行列式について扱います。
1. 行列式の定義
(1) 行列式の定義
以下の第3章の定義3.19とは異なり、より抽象的かつ一般的な定義を導入します。
- 線形性(multilinearity) 1つの列ベクトルに関して線形性を満たす。 例えば $k$ 列目が $\alpha\mathbf{u} + \beta\mathbf{v}$ に変わったとき、 $$ \det(\dots, \alpha\mathbf{u} + \beta\mathbf{v}, \dots) = \alpha\det(\dots, \mathbf{u}, \dots) + \beta\det(\dots, \mathbf{v}, \dots) $$
- 交代性(alternating property) 2つの列が等しい場合、その行列式は 0 である。また、2列を入れ替えると符号が反転する。 $$ \det(\dots, \mathbf{u}, \dots, \mathbf{u}, \dots) = 0, \quad \det(\dots, \mathbf{u}, \dots, \mathbf{v}, \dots) = -\det(\dots, \mathbf{v}, \dots, \mathbf{u}, \dots) $$
- 規格化(normalization) 単位行列の行列式は 1 とする。 $$ \det(I_n) = 1 $$
よく見かける符号($\mathrm{sgn}$)を用いた定義は上記の定義から導出が可能であり、次節で扱います。
(2) 行列式に関する定理(3):ベクトルのスカラー倍の行列式
証明をみる
行列式の線形性より明らか。(3) 行列式に関する定理(4):ベクトルを加えた行列式
証明をみる
線形性で分解し、交代性から追加項が0になる。(4) 行列式に関する定理(5):ベクトルを交換した行列式
証明をみる
行列式の交代性より明らか。(5) 行列式に関する定理(6):複数の同じベクトルの行列式
証明をみる
列 $p$ と列 $q$($p\neq q$)がまったく同じだとする。交代性により、これら2列を入れ替えると $$ \det(\dots,\text{列 }p,\dots,\text{列 }q,\dots) = -\det(\dots,\text{列 }q,\dots,\text{列 }p,\dots). $$ しかし「列 $p$ と列 $q$ は等しい」ので、入れ替えても行列そのものは変わらず、行列式の値も変わらない。よって $$ \det A = -\det A \quad\Rightarrow\quad \det A = 0. $$ より直観的には、2 本の同一列があると、体積(平行多面体の体積の一般化)が 0 になるためである。$\square$2. 符号による行列式の表現
以下の第3章の定義3.19を定義4.1から導出します。
(1) 単射の定義
(2) 全射の定義
(3) 全単射の定義
(4) 置換の定義
置換$\sigma$とは以下の性質を満たす写像のことです。
上記の置換の定義は抽象的で分かりづらいですが、結局のところ集合$X$から$X$への全単射として定められる写像$\sigma$は複雑ではなく、単に$X$の要素を並び替える写像のことです。
例えば集合$S_1=\{1, 2, 3, 4\}$に対し$1 \rightarrow 3$、$2 \rightarrow 1$、$3 \rightarrow 4$、$4 \rightarrow 2$に対応させる写像を$\sigma_1$とすると、$\sigma_1$は$S_1$から$S_1$への全単射写像の1つの例であるので$\sigma_1$は置換の1つです。これは$1, 2, 3, 4$を$3, 1, 4, 2$に並べ替える操作と同値です。
そこで、置換は以下のように表記します。上段に写像の元の要素を、下段に対応先の要素を記載します。
$$
\begin{pmatrix}
1 & 2 & 3 & 4 \\
3 & 1 & 4 & 2
\end{pmatrix}
$$
このように置換とは集合$S$について$S$の要素を並び替える写像とみなすことができ、順列の概念そのものです。従って、集合$S$の要素数を$n$とすると、$S$に対する置換は$n!$個存在します。
(5) 互換の定義
(6) 互換に関する定理(1):任意の置換は互換の合成で表現できる
互換と置換には以下の関係があります。
証明をみる
数学的帰納法で示す。集合$S$の要素数を$n$とする。$n=2$に対する置換は互換そのものであるため題意は自明。
$n>2$に対する置換については、例えば以下のように$n$を$n$に対応させるように1度互換を適用する。 $$ \begin{pmatrix} 1 & \cdots & n-1 & n \\ n & \cdots & 2 & n-1 \end{pmatrix} \rightarrow \begin{pmatrix} 1 & \cdots & n-1 & n \\ n-1 & \cdots & 2 & n \end{pmatrix} $$ すると残りは$n-1$までの集合に対する置換になるので、要素数が$n-1$に対する集合の置換が互換の組み合わせで構築できるならば要素数が$n$に対する集合の置換も互換の組み合わせで構築できることが分かる。
従って、題意成立。
(7) 符号の定義
(8) 符号に関する定理(1):符号は一意に定まる
置換を構成する互換の数が1通りと限らないことが想像できるため、符号の値が一意に定まるか自明ではありません。にもかかわず、置換に対して$-1$か$1$を一意に定めることができます。
また、$s$は$\mathrm{sgn}$の定義そのものである。
証明をみる
方針:ヴァンデルモンド積$$ \Delta(x_1,\dots,x_n):=\prod_{1 < k < l \leq n}(x_k-x_l) $$ を用いる。$\Delta$ は引数の交換で符号が反転する(交代式)ことから, $$ \Delta(x_{\sigma(1)},\dots,x_{\sigma(n)})=\mathrm{sgn}(\sigma)\,\Delta(x_1,\dots,x_n) $$ が成り立つ。一方, $$ \frac{\Delta(x_{\sigma(1)},\dots,x_{\sigma(n)})}{\Delta(x_1,\dots,x_n)} =\prod_{1 < k < l \leq n}\frac{x_{\sigma(k)}-x_{\sigma(l)}}{x_k-x_l} =s(\sigma) $$ なので,両式を比べれば $s(\sigma)=\mathrm{sgn}(\sigma)$ が従う。以下,この論法を丁寧に示す。
ステップ1:$\Delta$ は引数交換で符号が反転する(交代性)
2つの隣り合う引数 $x_i,x_{i+1}$ を入れ替える置換 $\tau=(i\ i\!+\!1)$ を考える。 $\Delta$ の各因子 $(x_k-x_l)$ のうち,この入れ替えで符号が変わるのは **ちょうど1つ**,すなわち $(k,l)=(i,i+1)$ の因子で,それが $(x_{i+1}-x_i)=-(x_i-x_{i+1})$ に変わる。他の因子は引数の並べ替えにより順番が入れ替わるだけで値は同じ(符号も不変)である。ゆえに $$ \Delta(\dots,x_{i+1},x_i,\dots)=-\,\Delta(\dots,x_i,x_{i+1},\dots). $$ 任意の置換は隣接交換の積に分解でき,交換1回につき符号が $-1$ ずつ掛かるので,一般に $$ \Delta(x_{\sigma(1)},\dots,x_{\sigma(n)})=\mathrm{sgn}(\sigma)\,\Delta(x_1,\dots,x_n). $$
ステップ2:$s(\sigma)$ はヴァンデルモンド比そのもの
定義から $$ \Delta(x_{\sigma(1)},\dots,x_{\sigma(n)}) =\prod_{1 < k < l \leq n}\bigl(x_{\sigma(k)}-x_{\sigma(l)}\bigr), $$ したがって $$ \frac{\Delta(x_{\sigma(1)},\dots,x_{\sigma(n)})}{\Delta(x_1,\dots,x_n)} =\prod_{1 < k < l \leq n}\frac{x_{\sigma(k)}-x_{\sigma(l)}}{x_k-x_l} = s(\sigma). $$
ステップ3:結論
ステップ1とステップ2より $$ s(\sigma) =\frac{\Delta(x_{\sigma(1)},\dots,x_{\sigma(n)})}{\Delta(x_1,\dots,x_n)} =\frac{\mathrm{sgn}(\sigma)\,\Delta(x_1,\dots,x_n)}{\Delta(x_1,\dots,x_n)} =\mathrm{sgn}(\sigma). $$ よって **$s(\sigma)=\mathrm{sgn}(\sigma)$** が示された。□
具体例をみる
例えば、 $$ \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ については、 $$ s(\sigma) = \frac{(x_3-x_2)(x_3-x_1)(x_2-x_1)}{(x_1 – x_2)(x_1 – x_3)(x_2 – x_3)} = -1 $$ となり、関数$s$によって任意の置換に$1$か$-1$を一意に定められることが分かります。以下は上記具体例のイメージ図です。
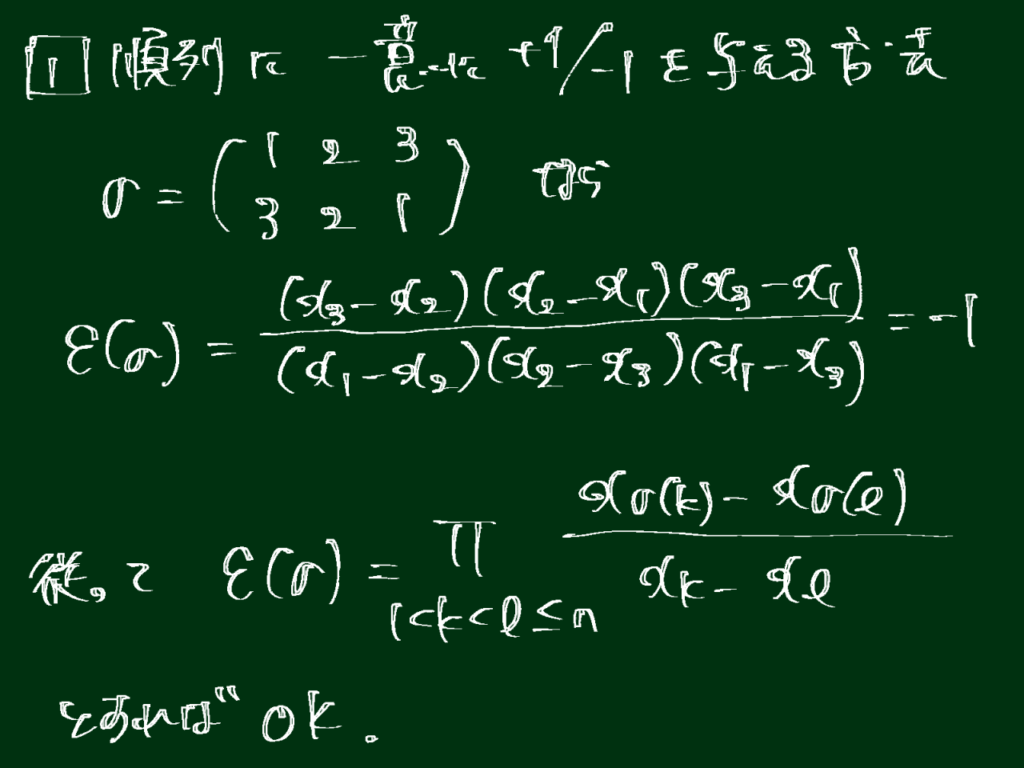
(8) 行列式に関する定理(7):符号($\mathrm{sgn}$)による表現 (再掲)
以下の記事の定義3.19を定理として扱い定義4.1に基づいて導出します。
記号の説明
- $S_n$:$n$ 個の要素 $\{1,2,\dots,n\}$ の全ての置換からなる集合。
- $\mathrm{sgn}(\sigma)$:置換 $\sigma$ の符号(sign)。
証明をみる
$A$ の各列を標準基底ベクトルの線形結合として書く。 $$ \text{第 }j\text{ 列}=\sum_{i=1}^n a_{ij}\,\mathbf{e}_i,\quad \mathbf{e}_i=(0,\dots,0,1,0,\dots,0)^T. $$ 行列式は各列に関して線形(多重線形)なので、$n$ 本の列すべてについて展開できる。 $$ \begin{align} \det A &= \det(\underbrace{\sum_{i_1} a_{i_1 1}\mathbf{e}_{i_1}}_{\text{第1列}}, \ \underbrace{\sum_{i_2} a_{i_2 2}\mathbf{e}_{i_2}}_{\text{第2列}}, \ \dots, \ \underbrace{\sum_{i_n} a_{i_n n}\mathbf{e}_{i_n}}_{\text{第n列}}) \\ &= \sum_{i_1=1}^{n} a_{i_1 1}\det(\mathbf{e}_{i_1},\ \sum_{i_2}a_{i_2 2}\mathbf{e}_{i_2},\ \sum_{i_n} a_{i_n n}\mathbf{e}_{i_n}) \\ &= \sum_{i_1=1}^{n} a_{i_1 1}\Big(\sum_{i_2=1}^{n} a_{i_2 2} \det(\mathbf{e}_{i_1},\ \mathbf{e}_{i_2},\ \sum_{i_n} a_{i_n n}\mathbf{e}_{i_n})\Big) \\ &= \sum_{i_1=1}^{n} \sum_{i_2=1}^{n} a_{i_1 1}a_{i_2 2}\det(\mathbf{e}_{i_1},\ \mathbf{e}_{i_2},\ \sum_{i_n} a_{i_n n}\mathbf{e}_{i_n}) \\ &= \sum_{i_1=1}^{n} \sum_{i_2=1}^{n} \sum_{i_3=1}^{n} a_{i_1 1}a_{i_2 2}a_{i_3 3}\det(\mathbf{e}_{i_1},\ \mathbf{e}_{i_2},\ \mathbf{e}_{i_3},\ \sum_{i_n} a_{i_n n}\mathbf{e}_{i_n}) \\ &= \sum_{i_1=1}^{n} \sum_{i_2=1}^{n} \cdots \sum_{i_n=1}^{n} a_{i_1 1}a_{i_2 2} \cdots a_{i_n n}\det(\mathbf{e}_{i_1},\ \mathbf{e}_{i_2},\ \cdots \mathbf{e}_{i_n}) \\ &= \sum_{i_1=1}^{n} \sum_{i_2=1}^{n} \cdots \sum_{i_n=1}^{n} \Big(\prod_{j=1}^n a_{i_j j}\det(\mathbf{e}_{i_1},\dots,\mathbf{e}_{i_n})\Big) \\ &= \sum_{i_1,\dots,i_n}\Big(\prod_{j=1}^n a_{i_j j}\Big)\det(\mathbf{e}_{i_1},\dots,\mathbf{e}_{i_n}) \end{align} $$ ここで 交代性 を使う。もし $i_p=i_q$(同じ基底ベクトルが2回以上出現)なら、2列が等しいため $\det(\mathbf{e}_{i_1},\dots,\mathbf{e}_{i_n})=0$。 よって 非零になりうるのは $i_1,\dots,i_n$ が $1,\dots,n$ を重複なく並べ替えた場合、すなわち 集合$S = \{1, 2, \cdots, n\}$の置換$\sigma$になっている場合に限られる。したがって、$S$の置換全体の集合を$S_n$と表記することで、以下のように変形が可能。 $$ \sum_{i_1,\dots,i_n}\Big(\prod_{j=1}^n a_{i_j j}\Big)\det(\mathbf{e}_{i_1},\dots,\mathbf{e}_{i_n}) = \sum_{\sigma\in S_n}\Big(\prod_{j=1}^n a_{\sigma(j),\,j}\Big)\det(\mathbf{e}_{\sigma(1)},\dots,\mathbf{e}_{\sigma(n)}) $$ 最後に 規格化 と 交代性 を合わせて、 $$ \det(\mathbf{e}_{\sigma(1)},\dots,\mathbf{e}_{\sigma(n)})=\mathrm{sgn}(\sigma)\,\det(\mathbf{e}_1,\dots,\mathbf{e}_n)=\mathrm{sgn}(\sigma)\cdot 1 $$ が分かる(置換で列を入れ替えると符号が $\mathrm{sgn}(\sigma)$ 倍され、単位行列の行列式は 1)。以上より $$ \det A=\sum_{\sigma\in S_n}\mathrm{sgn}(\sigma)\,a_{1\sigma(1)}a_{2\sigma(2)}\cdots a_{n\sigma(n)} $$ が導かれる。$\square$具体例をみる
以下の3次正方行列$A$の行列式を考える。 $$ \begin{pmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{pmatrix} $$$n=3$ の置換全体の集合$S_3$ には以下の合計$3!=6$ 個の置換が存在する。
$$ \sigma_1 = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 2 & 3 \end{pmatrix}, \sigma_2 = \begin{pmatrix} 1 & 2 & 3 \\ 1 & 3 & 2 \end{pmatrix}, \sigma_3 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 3 \end{pmatrix} $$ $$ \sigma_4 = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \end{pmatrix}, \sigma_5 = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \end{pmatrix}, \sigma_6 = \begin{pmatrix} 1 & 2 & 3 \\ 3 & 2 & 1 \end{pmatrix} $$ 従って、 $$ \begin{align} \det A &=\sum_{\sigma\in S_3} \mathrm{sgn}(\sigma)\prod_{i=1}^{3} a_{i,\sigma(i)} \\ &= \mathrm{sgn}(\sigma_1)\prod_{i=1}^{3} a_{i,\sigma_1(i)} + \cdots + \mathrm{sgn}(\sigma_6)\prod_{i=1}^{3} a_{i,\sigma_6(i)} \\ &= 1 \times a_{1,\sigma_1(1)}a_{2,\sigma_1(2)}a_{3,\sigma_1(3)} + \cdots + (-1) \times a_{1,\sigma_6(1)}a_{2,\sigma_6(2)}a_{3,\sigma_6(3)} \\ &= a_{11}a_{22}a_{33} – a_{11}a_{23}a_{32} – a_{12}a_{21}a_{33} + a_{12}a_{23}a_{31} + a_{13}a_{21}a_{32} -a_{13}a_{22}a_{31} \end{align} $$
3. 余因子展開による行列式の表現
(1) 行列式に関する定理(8):余因子展開による表現
また、$C_{ij}$を$ij$に関する余因子という。
証明をみる
$i$ 行(横ベクトル)を標準基底ベクトルの線形結合に分解する。第 $i$ 行は $$ (a_{i1},a_{i2},\dots,a_{in}) =\sum_{j=1}^n a_{ij}\,\mathbf{e}_j^{\top} $$ と書けるから、行列式の $i$ 行に関する線形性より $$ \begin{align} \det A&= \det\begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \vdots & \cdots \\ a_{i1} & 0 & 0 \\ \vdots & \vdots & \cdots \\ a_{n1} & \cdots & a_{nn} \\ \end{pmatrix} + \cdots + \det\begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \vdots & \cdots \\ 0 & 0 & a_{in} \\ \vdots & \vdots & \cdots \\ a_{n1} & \cdots & a_{nn} \\ \end{pmatrix} \\ &= a_{i1} \det\begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \vdots & \cdots \\ 1 & 0 & 0 \\ \vdots & \vdots & \cdots \\ a_{n1} & \cdots & a_{nn} \\ \end{pmatrix} + \cdots + a_{in} \det\begin{pmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & \vdots & \cdots \\ 0 & 0 & 1 \\ \vdots & \vdots & \cdots \\ a_{n1} & \cdots & a_{nn} \\ \end{pmatrix} \\ &=\sum_{j=1}^n a_{ij}\,\det(A\ \text{の }i\text{ 行を }\mathbf{e}_j^{\top}\text{ に置き換えた行列}) \end{align} $$ となる。ここで、以下のように第$i$行を$1$行目に移動させた後に、$1$行目に$1$が立っている列を$1$列目まで移動させる操作を考える。
$$ \begin{pmatrix} * & * & * & * & * \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & \cdots & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ * & * & * & * & * \\ \end{pmatrix} \\ \rightarrow \begin{pmatrix} 0 & \cdots & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ * & * & * & * & * \\ \end{pmatrix} \\ \rightarrow \begin{pmatrix} 1 & \cdots & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ * & * & * & * & * \\ \end{pmatrix} \\ = \begin{pmatrix} 1 & 0 \\ * & M_{ij} \\ \end{pmatrix} $$
$i$ 行を$1$行目まで行の入れ替えで移動させるためには$(i-1)$回の入れ替えが、$j$列目を$1$列目まで列の入れ替えで移動させるためには$(j-1)$回の入れ替えが必要。
なお、上記の入れ替え回数は隣同士の行または列の入れ替えを想定していることに注意。仮に$i$行目と$1$行目を直接入れ替えると、残った部分の行列の行の順序が保たれず、小行列$M_{ij}$が現れない。
よって、合計 $(i-1)+(j-1)$ 回 の入れ替えが必要(合計 $i+j-2$ 回)。入れ替え1回につき符号が $-1$ 倍されるので、全体で $(-1)^{i+j}$ が出る。
また、入れ替えが終わった行列の行列式は、行列式の符号による表現から、以下のように小行列の行列式と等しい。ただし$S_1$を$S_n$のうち1から始まる順列全体の集合、$S_x$を$S_n$のうち1から始まらない順列全体の集合とする。
$$ \det \Big( \begin{pmatrix} a_{11} & 0 \\ * & M_{ij} \\ \end{pmatrix} \Big) = \sum_{\sigma \in S_1} \mathrm{sgn}(\sigma) a_{11}\prod_{i=2}^{n} a_{i,\sigma(i)} + \sum_{\sigma \in S_x} \mathrm{sgn}(\sigma) a_{1\sigma{1}}\prod_{i=2}^{n} a_{i,\sigma(i)} \\ = a_{11} * \det(M_{ij}) + \sum_{\sigma \in S_x} \mathrm{sgn}(\sigma) a_{1\sigma{1}}\prod_{i=2}^{n} a_{i,\sigma(i)} \\ = 1 \times \det(M_{ij}) + \sum_{\sigma \in S_x} \mathrm{sgn}(\sigma) \times 0 \times \prod_{i=2}^{n} a_{i,\sigma(i)} \\ = \det(M_{ij}) $$
以上より
$$ \det A=\sum_{j=1}^n a_{ij}\,(-1)^{i+j}\,M_{ij} $$ が従う。列に沿う展開も同様に示せる。$\square$
(2) ベクトル値ラプラス展開
行列式の余因子展開を用いて、以下のように成分にベクトルが含まれた行列の行列式の定義があります。これは外積を表現する際に便利な表記です。
(3) ベクトル値ラプラス展開の性質
2×2 行列式の交代性・線形性が各成分でき、それを基底で足し合わせるだけなので、$\mathcal{D}$ 全体としても 反対称・各引数について線形になります。従って、以下が成立します。
$\alpha, \beta \in \mathbb{R},\, \mathbf{a}_1, \mathbf{a}_2, \mathbf{a}, \mathbf{b}_1, \mathbf{b}_2, \mathbf{b} \in \mathbb{R}^3$としたとき、ベクトル値ラプラス展開について以下の性質が成立します。
- $\mathcal{D}(\mathbf{a}, \mathbf{b}) = – \mathcal{D}(\mathbf{b}, \mathbf{a})$
- $\mathcal{D}(\mathbf{a}, \mathbf{a}) = \mathbf{0}$
- $\mathcal{D}(\alpha\mathbf{a}_1+\beta\mathbf{a}_2, \mathbf{b}) = \alpha\mathcal{D}(\mathbf{a}_1, \mathbf{b})+\beta\mathcal{D}(\mathbf{a}_2, \mathbf{b})$
- $\mathcal{D}(\mathbf{a}, \alpha\mathbf{b}_1+\beta\mathbf{b}_2) = \alpha\mathcal{D}(\mathbf{a}, \mathbf{b}_1)+\beta\mathcal{D}(\mathbf{a}, \mathbf{b}_2)$
4. 行列式に関する定理
(1) 行列式に関する定理(9):積の行列式
証明をみる (行列式の定義を利用)
$B$ の列ベクトルを $\mathbf{b}_1,\dots,\mathbf{b}_n$ とし、$F(B):=\det(AB)$ とおく。$F$ を「$B$ の列に関する関数」と見て、行列式を特徴づける条件を調べる。多重線形性
$B = (\mathbf{b}_1, \cdots, \mathbf{b}_n)$とすると、$AB = (A\mathbf{b}_1, \cdots, A\mathbf{b}_n)$。$\mathbf{b}_i = \alpha\mathbf{u} + \beta\mathbf{v}$とすると、以下となる。 $$ \begin{align} F(B) &= F(\mathbf{b}_1, \cdots, \alpha\mathbf{u}+\beta\mathbf{v}, \cdots, \mathbf{b}_n) \\ &= \det(A\mathbf{b}_1, \cdots, A(\alpha\mathbf{u}+\beta\mathbf{v}), \cdots, A\mathbf{b}_n) \\ &= \det(A\mathbf{b}_1, \cdots, \alpha A\mathbf{u}+\beta A\mathbf{v}, \cdots, A\mathbf{b}_n) \\ &= \alpha\det(A\mathbf{b}_1, \cdots, A\mathbf{u}, \cdots, A\mathbf{b}_n)+\beta\det(A\mathbf{b}_1, \cdots, A\mathbf{v}, \cdots, A\mathbf{b}_n) \\ &= \alpha A(\mathbf{b}_1, \cdots, \mathbf{u}, \cdots, \mathbf{b}_n) + \beta A(\mathbf{b}_1, \cdots, \mathbf{v}, \cdots, \mathbf{b}_n) \\ &= \alpha F(\mathbf{b}_1, \cdots, \mathbf{u}, \cdots, \mathbf{b}_n) + \beta F(\mathbf{b}_1, \cdots, \mathbf{v}, \cdots, \mathbf{b}_n) \end{align} $$ 従って、 $$ F(\mathbf{b}_1, \cdots, \alpha\mathbf{u}+\beta\mathbf{v}, \cdots, \mathbf{b}_n) = \alpha F(\mathbf{b}_1, \cdots, \mathbf{u}, \cdots, \mathbf{b}_n) + \beta F(\mathbf{b}_1, \cdots, \mathbf{v}, \cdots, \mathbf{b}_n) $$ となるから、Fは(多重)線形性を満たす。
交代性
$B$ の2列が等しければ $A$ を掛けた後も 2 列は等しい。すると行列式は 0。列の入れ替えでも符号が反転。したがって $F$ は交代的。
Bについて上記の2つの性質を満たす関数は$k \det B$以外にはないが、$B=I$とすることで$k=\det A$がわかり、結局$\det(AB)=\det(A)\det(B)$。
証明をみる (符号による行列式の表現を利用)
$$ \begin{align} \det(AB) = \det(A\mathrm{b}_1, \cdots, A\mathrm{b}_n) &= \det(\sum_{i_1=1}^n b_{i_1, 1}A\mathbf{e_{i_1}}, \cdots, \sum_{i_n=1}^n b_{i_1, n}A\mathbf{e_{i_n}}) \\ &= \sum_{i_1, \cdots, i_n} \prod_{j=1}^n b_{i_j, j} \det(A\mathrm{e_{i_1}}, \cdots, A\mathrm{e_{i_n}}) \\ &= \sum_{\sigma \in Sn}\mathrm{sgn}(\sigma)\prod_{i=1}^n b_{i,\sigma{i}} \det(A\mathrm{e}_1, \cdots, A\mathrm{e}_n) \\ &= \det(B)\det(AE) \\ &= \det(A)\det(B) \end{align} $$ となる。$\square$(2) 行列式に関する定理(10):三角行列の行列式
証明をみる
ここでは、$n \times n$ の上三角行列の場合を考える(下三角行列も同様の議論で示せる)。 上三角行列 $U$ を $$ U = \begin{pmatrix} u_{11} & u_{12} & \cdots & u_{1n} \\ 0 & u_{22} & \cdots & u_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & u_{nn} \end{pmatrix} $$ とする。行列式の定義は置換 $\sigma$ を用いて次のように書ける: $$ \det(U) = \sum_{\sigma \in S_n} \mathrm{sgn}(\sigma) \prod_{i=1}^n u_{i,\sigma(i)} $$ ここで、$S_n$ は $\{1,2,\ldots,n\}$ の全ての置換の集合、$\mathrm{sgn}(\sigma)$ は置換の符号である。
ステップ 1: 非対角要素のゼロの影響
$U$ は上三角行列なので、$i > j$ のとき $u_{ij} = 0$ である。
積 $\prod_{i=1}^n u_{i,\sigma(i)}$ がゼロでないためには、各 $i$ に対して $\sigma(i) \geq i$ が成り立つ必要がある。
なぜなら、もし $\sigma(i) < i$ となると $u_{i,\sigma(i)} = 0$ となり、その積全体がゼロになるからである。
ステップ 2: ゼロでない項が現れる条件
$\sigma(i) \geq i$ をすべての $i$ について満たす置換は、恒等置換 $\sigma = \mathrm{id}$ しか存在しない。
これは次の理由による:
– $\sigma(1) \geq 1$ より $\sigma(1) = 1$ でないと、残りの行で条件を満たせない。
– $\sigma(2) \geq 2$ より $\sigma(2) = 2$。
– …と順に適用すると、最終的に $\sigma(i) = i$ がすべての $i$ に対して成立。
ステップ 3: 恒等置換の場合の積
恒等置換 $\sigma = \mathrm{id}$ の場合、置換の符号は $\mathrm{sgn}(\mathrm{id}) = 1$ であり、 $$ \prod_{i=1}^n u_{i,\sigma(i)} = \prod_{i=1}^n u_{ii} $$ となる。
ステップ 4: 結論
したがって、 $$ \det(U) = \prod_{i=1}^n u_{ii} $$ が成り立つ。
(3) 行列式に関する定理(11):アダマールの不等式
証明をみる
1. QR分解列 $\mathbf{a}_1,\dots,\mathbf{a}_n$ に Gram–Schmidt を施すと、直交行列 $Q$ と上三角行列 $R$ が得られ、$A=QR$。ここで $Q$ は列が直交・正規化($|Q\mathbf{e}_j|=1$)されており、$R$ は上三角。
※ QR分解については以下。
2. 行列式の分解
$\det A=\det(Q)\det(R)$。直交行列は体積を保存するので $|\det(Q)|=1$。
これは、直交行列の固有値は1であり、固有値の積が行列式となることから分かります。
(1) 直交行列の固有値については以下の記事を参照して下さい。
Gram–Schmidt の構造から、$Q=(\mathrm{q}_1, \cdots, \mathrm{q}_n)$とおくと、 $$ \begin{align} r_{jj} &= \|\mathrm{a_{j}} – \sum_{i=1}^{j-1}(\mathrm{q}_j^T \mathrm{a_{j}})\mathrm{q}_j\| \\ &= \|\mathbf{a}_j^\perp\| \end{align} $$ となる。$\|\mathbf{a}_j^\perp\|$は$\mathbf{a}_j$ を既に作った直交基底が張る空間へ射影した成分のノルムであるため、必ず$|\mathbf{a}_j^\perp|\ \le\ |\mathbf{a}_j|$となる。従って、 $$ \det A=\prod_{j=1}^n |r_{jj}|\ \le\ \prod_{j=1}^n |\mathbf{a}_j|. $$ 4. 等号成立条件
等号が成立するには各 $j$ で $|\mathbf{a}_j^\perp|=|\mathbf{a}_j|$、すなわち $\mathbf{a}_j$ がそれ以前の列の張る空間に全く射影を持たない必要がある。これは列が相互に直交していることと同値。








コメント